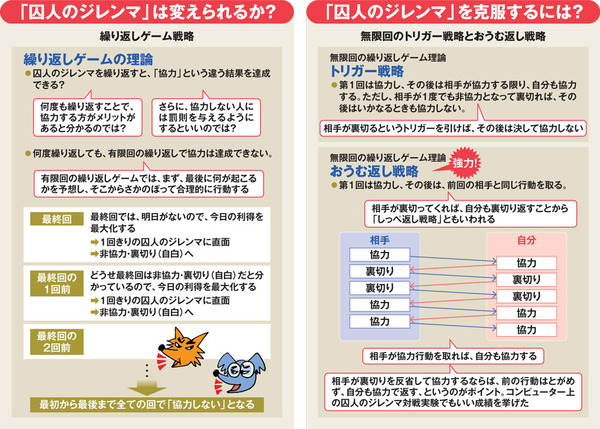
1回きりではなかなか黙秘(協力)とはならない囚人だが、100回、200回と繰り返しても、有限回である限り協力は達成されないとされる。
理論による説明はこうだ。繰り返しゲームには、最後の1回が必ずある。それまでの回で何をしてこようと、この回の利得を最大化しようとするため、通常の囚人のジレンマに直面する。つまりは、最後の回は絶対に協力しない。100回ゲームなら100回目は裏切り(自白)と決まる。
1回前の99回目はどうか。100回目は裏切りと決まっているので、99回目にはその回の利得を最大化しようと、裏切ることになる。
かくして98回目、97回目と逆算するように考えていくと、理論的には最初から最後まで全ての回で裏切ることとなる。
これに対し、後ろから逆に考えることのできない無限の繰り返しゲームでは、理論的に協力が達成されることが分かっている。相手が一度でも裏切れば、こちらもずっと裏切り続ける「トリガー戦略」などによって、協力が得られるというのである。
だが、こうした無限の繰り返しゲームというものは現実にはあり得ない。有限回の繰り返しでは、協力関係は生まれないのか。実は可能なことがさまざまな実験によって明らかになっている。
ここで力を発揮するのは「おうむ返し戦略」だ。1回目は協力し、それ以降は相手をまねするように、相手が協力したら協力し、協力しなければこちらもしない。
囚人には裏切りたいインセンティブが常にある。しかし、得をしても次の回には裏切られ、ダメージを食らう。1回だけ得をしても意味がないことを学習していく。
1980年代のこと、米国の政治学者のアクセルロッドがさまざまな分野の研究者を集めて囚人のジレンマを対戦させ、獲得した点数を競うコンピュータープログラム選手権を開催した。ここで優勝したのは、このおうむ返し戦略だったのである。プログラム自体も簡単なものだった。
結局のところ勝利を手にしたのは、シンプルなルールで正直に動き、協力関係を築いた戦略だったという実験結果は示唆に富む。



