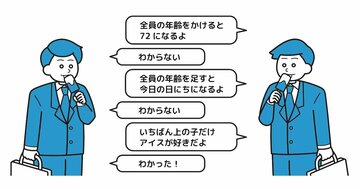
2試合目で負けたのはA
それぞれの合計試合数しかわからないのに、いきなり「第2試合」の結果を聞かれて驚いたかと思います。
難易度は「ふつう」ですが、ちょっと難しいかもしれません。
最初の着眼点さえ見つかれば、あとは流れるように解けていきます。
おこなわれた試合の「合計数」がわかる
順を追って考えていきましょう。
唯一わかっている手がかりは、3人それぞれの合計試合数です。
どうやらここから、別の情報を得る必要がありそうです。
3人がおこなった試合数を、合計してみましょう。
つまり合計42試合がおこなわれた……ように思えますが、違います。
シングル戦は1対1。
2人でおこなわれるので、1試合につき2人の試合数が重複してカウントされます。
そのため、「42÷2=21」が全体としておこなわれた試合数です。
卓球の試合は計21回おこなわれたと判明しました。
実現可能な「最大」の試合数とは？
ここまでに判明している事実は、全体の試合数が21回であることと、「3人の試合数に偏りがある」ことです。
しかし、これだけでは答えは出ません。
思考の糸口が見えないときは、
まずは上限と下限の数値を求めてみると、手がかりが見えてくることがあります。
参加者の1人が可能な「最大の試合数」を考えてみましょう。
これは簡単ですね。1試合目から参加して、全勝することです。
つまり、
21試合が「理論上可能な最大試合数」
だとわかります。
では、実現可能な「最小」の試合数とは？
では反対に、「理論上可能な最小試合数」は？
これを実現する方法は、「毎回かならず敗北する」ことです。
毎回負けて、次の試合には出ないことで、なるべく少ない試合数で21試合を乗り切れます。
「毎回かならず敗北する」ということは、たとえば1試合目は出て、2試合目は休んで、3試合目は出て……といった具合になるので、
1、3、5、7、9、11、13、15、17、19、21（計11試合）
2、4、6、8、10、12、14、16、18、20（計10試合）
という出場履歴になります。
つまり理論上可能な試合の最小回数は「10試合」です。
毎回かならず敗北することでのみ、この結果が得られます。
10試合しか出場しなかったAの存在
理論上可能な試合の最小回数と、その場合の戦績がわかりました。
お気づきでしょうか。
10試合しかしていない人が、3人のなかにいましたね。
すなわち、試合数が10だったAは、この戦績だったとわかります。
毎回かならず敗北していたわけです。
そして問題文で聞かれているのは「2試合目で負けたのは誰か」です。
Aの試合数が10試合になるのは、2試合目から出場し、すべての試合で敗北した場合だけ。
つまり、2試合目で負けたのはAです。
「思考」のまとめ
「試しに最大値と最小値を求めてみる」というのは、よくある解決手段です。
私も仕事において、あらゆる可能性が考えられるようなときは、まずは「考えるべき範囲を絞る」ことを習慣にしています（実際にできているかと聞かれると自信はありませんが……）。
「もっと難しくても大丈夫」という方は、そのうち紹介する上級問題「隠された運動会」にも挑戦してみてください。
きっと、楽しめると思います。
・思考のとっかかりがつかめないときは、まずは「最大」「最小」といった極端な場合から考えてみる
（本稿は、『頭のいい人だけが解ける論理的思考問題』から一部抜粋した内容です。）
都内上場企業のWebマーケター。論理的思考問題を紹介する国内有数のブログ「明日は未来だ！」運営者
ブログの最高月間PVは70万超。解説のわかりやすさに定評があり、多くの企業、教育機関、テレビ局などから「ブログの内容を使わせてほしい」と連絡を受ける。29歳までフリーター生活をしていたが、同ブログがきっかけとなり広告代理店に入社。論理的思考問題で培った思考力を駆使してWebマーケティングを展開し、1日のWeb広告収入として当時は前例のなかった粗利1500万円を達成するなど活躍。3年間で個人利益1億円を上げた後、フリーランスとなり、企業のデジタル集客、市場分析、ターゲット設定、広告の制作や運用、セミナー主催など、マーケティング全般を支援する。2023年に現在の会社に入社。Webマーケティングに加えて新規事業開発にも携わりながら、成果を出している。本書が初の著書となる。
連続大重版!!
大人も子供も、ハマる人続出!!
あっという間に15万部突破!!
読むほどに「地頭力」が高まると話題!!
世界レベルの考える力が身につく「最高の知的トレーニング本」
★Google、Apple、Microsoft、米国国家安全保障局が採用試験で出題!! ★
★知識や計算はいっさい不要!! 問われるのは「考える力」のみ!! ★
★読むだけで「地頭力」がおのずと磨かれる!! ★
★古典的名作から、SNSで度々バズる話題作まで、世界中から良問を収集!! ★
★論理的思考・批判思考・水平思考・俯瞰思考・多面的思考を高める67問 ★
論理的思考問題とは、知識や計算を必要とせず、
「考える力」さえあれば正解を導ける問題を指します。
直感で考えると、間違えてしまう。
でも、ちゃんと考えると答えがわかる。
この本は、そんな問題をとおして読者の「地頭力」を高めていきます。
娯楽としてではなく、仕事や人生において「論理的に考える力」を養う本です。
たとえ解けなくても、解説を読んで理解するだけで「思考回路」が構築されていきます。
さあ、世界のエリートがたしなむ「最高の知的トレーニング」に挑んでみましょう。
本書の目次
第1章：論理的思考のある人だけが解ける問題
矛盾のない真実を導けるか？ ――「3人の村人」
論理の力で盲点に気づけるか？ ――「3つの調味料」
裏の裏まで考えられるか？ ――「天国への道」
事実を抽象化して考えられるか？ ――「50%の帽子」
法則の攻略法を見抜けるか？ ――「シュレディンガーの猫」 など、12問
第2章：批判思考のある人だけが解ける問題
事実を疑って考えられるか？ ――「消えた1000円」
直感の落とし穴に気づけるか？ ――「2回目の競走」
思考の盲点に気づけるか？ ――「すれ違う船の謎」
「数字」の罠を見抜けるか？ ――「不思議な給料アップ」
仕組まれた戦略に気づけるか？ ――「三つどもえの選挙戦」
すべてを疑う勇気はあるか？ ――「正直者と嘘つきの島」 など、14問
第3章：水平思考のある人だけが解ける問題
やわらかい頭で考えられるか？ ――「熊の色は?」
先入観を捨てた発想ができるか？ ――「2本の線香」
解決すべき「真因」に気づけるか？ ――「4つのボート」
逆転の発想をする力はあるか？ ――「のろのろ馬レース」
狭い視野から抜け出せるか？ ――「天秤と9枚の金貨」
あらゆる情報を発想の糧にできるか？ ――「投票結果のカウント」 など、13問
第4章：俯瞰思考のある人だけが解ける問題
冷静に状況を俯瞰できるか？ ――「3つのフルーツボックス」
隠された事実を炙り出せるか？ ――「見落とした印刷ミス」
時間を超えて状況を俯瞰できるか？ ――「異国のレストラン」
状況が示す意味を見抜けるか？ ――「赤青のマーク」
他者の思惑まで俯瞰できるか？ ――「ダイヤル錠の部屋」
思考の闇を手探りで進んでいけるか？ ――「隠された運動会」 など、12問
第5章：多面的思考のある人だけが解ける問題
視点を変えて考えられるか？ ――「泥のついた2人」
他者の思考を読み取れるか？ ――「髪が乱れた3人」
未来の展開を見通せるか？ ――「3人の射撃戦」
「もしも」の「もしも」まで考えられるか？ ――「8枚の切手」
何手も先の思考を読み取れるか？ ――「ドラゴンの島」 など、12問
第6章：すべてのはじまりになった問題
すべての論理的思考を総動員できるか？ ――「石像の部屋」
