チャートは相場の「全てを語る」のか？
それともチャートは「オカルト」なのか？（2）

チャートパターンの多くは幻想であり、チャートが当たっているように見えるのは後付け効果によるものだ。人はチャートの中に、自分自身の心理を映し出しているだけなのである。それにもかかわらず、多くの成功したトレーダーたちは、ファンダメンタルズ以上にチャートを重視している。トレードのチャンスを機敏に見つけるのに、それ以外の方法がないからである。
――「なぜ、投資で勝つことは難しいのか？」という根本的な疑問に答えながら「金融市場の全体像」を示していく好著として、発売直後から絶賛される『投資と金融にまつわる12の致命的な誤解について』より、投資家の関心が高い「チャート」の真実に迫る章を全文公開する連載の第2回。

“パターン”をめぐる永遠の戦い

 ここまで、チャート分析の有効性が実にあやふやなものであることを見てきた。結局のところ、少なくともよく知られているチャート分析手法の成績は、どれも当たったり外れたりだ。だが、これでチャート分析の有効性が完全に否定されるわけではない。

 チャート分析が有効であるためには、100％当たる必要はない。人は、どうしても必勝法を追い求めたがるのであるが、予測不能性が付きまとう市場にはそんなものは存在しない。全ては当たったり外れたりするのだ。だが、当たったり外れたりが完全にフィフティ・フィフティであることと、55％とか60％は当たって、残りが外れるのとでは大きく意味が違う。ちなみに、表裏が出る確率がそれぞれ50％のコイン投げをしていても、試行回数が少なければどちらかが出る確率が高いように見えることもある。ここで言っている確率とはそういうものではなく、無限回試したときに現れる本当の確率のことである。現実には無限回試行することなどできないので、本当の確率を知ること自体がとても難しいのだが、ここではそれがわかるとしよう。

 さて、そうした意味での本当の勝率が60％のチャート分析手法があったとする。1回限りの勝負なら勝つ確率はそのまま60％だが、3回勝負してそのうち2回以上勝つ確率は約65％となる。同様に、5回勝負して勝ち越す確率は約68％、11回勝負なら約75％へと上がっていく。要するに、勝つ確率が50％を超えるやり方を見つけて数多く試せば、勝ち越す確率はどんどん高くなっていくのだ。だから、本当に50％以上の確率で勝てる方法があるのなら、それは投資の世界ではとても大きな発見となる。

 当たったり外れたりとはいっても、こうしたちょっと勝率が良いくらいのやり方なら存在するのではないか。市場が完全にランダムでないとしたら、そう考えることは決して不自然ではないはずだ。幻想にとらわれていない真のチャート分析のプロが目指しているのは、まさにそういうことだ。

 だが、ここでも1万円札の法則が大きく立ちはだかる。有利な取引機会をめぐる競争によって、その有利な取引機会が存在する時間はどんどん短くなり、やがて消滅してしまうという法則だ。

 少し簡単な例を取り上げてみよう。日経平均株価の過去データを分析したところ、過去5日の移動平均値が過去25日の移動平均値を上回ったら、その後しばらくの間は相場が上昇しやすいことがわかったとしよう（これが、本当に意味のある法則なのか、単なる偶然の産物を誤認したものであるのかはここでは問わない）。

 テクニカル分析は世界中で大勢の投資家がしのぎを削っているため、このような簡単な法則が利益を生むとなれば、彼らの多くが次第にその存在に気が付くようになっていくはずだ。そうすると、やがて買いサインが出たときに大勢の投資家が一斉に買い行動を起こして、価格が急上昇するようになる。あるチャート分析が広まることにより、そのチャート分析の有効性が高まっていくわけだ。だが、投資家たちは他の投資家よりもいち早く行動を起こして少しでも利益を膨らませたいと競争するため、やがて価格が短時間で急上昇して、その後は買いが続かないという状態になっていく。トレンドは、有利な取引タイミングの判断が投資家によって異なるときに、大勢の投資家が時間をかけて順次ゆっくりと行動を起こすことで形成される。しかし、有利な取引タイミングが誰の目にも明らかならば、そこに投資家が殺到するため、持続的な動きとはならない。結局、大きな値上がりが一瞬起きるだけで終わってしまう。

 話はここでとどまらない。値上がりが一瞬しか起こらないことも、やがて多くの投資家が認識することになる。そうすると、値上がりしたらすぐに利益を確定させるための売りを出す投資家が増え、やがてここでも競争が高まって、価格上昇はどんどん短くなり、やがて一時的な価格上昇すら起こらなくなっていく。

 こうして、大勢の投資家が気付くことによって、そのチャート分析はまったく意味のないものになっていく。これが、チャート分析の宿命なのだ。そして、誰もが知っているチャート分析は有効性を失い、目端の利く投資家は、もっと複雑で、簡単には他の投資家が気付かないパターンを探すことになる。だが、やがて複雑なパターン探しについても競争が起き、そのスピードを競うためにコンピュータープログラムによる計算が使われるようになって、やがて複雑なチャート分析も効力を失っていく。つまり、チャート分析の進化によって、多くのチャート分析は有効性を失っていき、市場は効率性を増していくことになる。

 もちろん、常に新しいパターンを探し続けることによって、まだ誰も気付いていない投資機会を発見できることもあるだろう。だが、その有効性も永くは続かない。そして、次の投資機会を探しに行かなくてはならない。有効なパターン探しは、永遠に続くモグラたたきのようなものなのである。

数に備わる神秘とチャート教

 これまで見てきたように、チャート分析の大半は、結局のところ、思い込みや幻想によるものである。たとえごくわずかに有効性があったとしても、持続性はなく、常に新しいパターンを探し続けなければならない。つまり、必勝法はどこにも存在しない。

 それでも、チャート分析には、人を引き付けてやまないもう1つの魅力が備わっている。それは、数字の神秘に起因するものだ。

 古代から、数字に秘められた神秘的な性質に取りつかれた人は数多い。有名な古代ギリシャのピタゴラスは、「アルケーは数である」とした。アルケーとは、万物の根源という意味だ。宇宙の真理や秩序は、数字の中に表れるということだ。ピタゴラスは数学者として歴史に名を刻んでいるが、彼の学派は神秘的な宗教色を強く帯びていて（※）、ピタゴラス教団とも言われていた。

※ピタゴラスの学派は、宗教的色彩を帯びた秘密結社を結成していて、その教義は外部には秘密とされた。分数で表すことのできる有理数のみを数とし、分数で表すことのできない無理数の存在を認めていなかったため、無理数を発見した弟子を殺害したというエピソードさえ伝えられている。

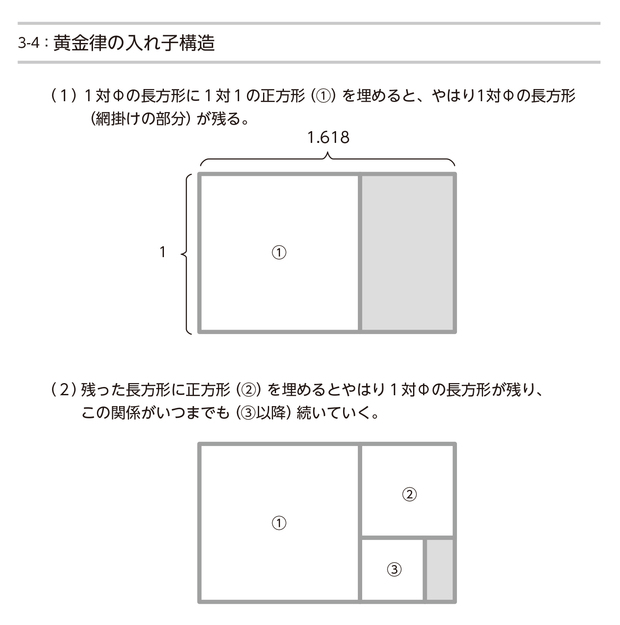
 数字の神秘の中でも最もよく知られるものは黄金律（Φ、ファイ）だろう。（1＋ルート5）÷2であらわされる数字だ。黄金律は、視覚的に最も美しいバランスをもたらす比率として、建築や美術作品に多く取り入れられている。また、1をΦで割るとΦ－1になるというように、入れ子構造のような秩序だった法則が現れることでも知られる。図3－4は、短辺と長編が1：Φになっている長方形の中に正方形を埋めていくと、Φ分の1ずつ辺が短い正方形によって埋まっていくという構造が永遠に続いていくことを示している。これもその入れ子構造的秩序によるものだ。

 
 フィボナッチ数も、神秘的な数として有名なものだ。1、2、3（＝1＋2）、5（＝2＋3）、8（＝3＋5）というように、隣り合う2つの数を足し合わせることで生成される数列で表されるものがフィボナッチ数だ。フィボナッチ数列の隣り合う2つの数字の比率は、次第に黄金律に近づいていくことがわかっている。

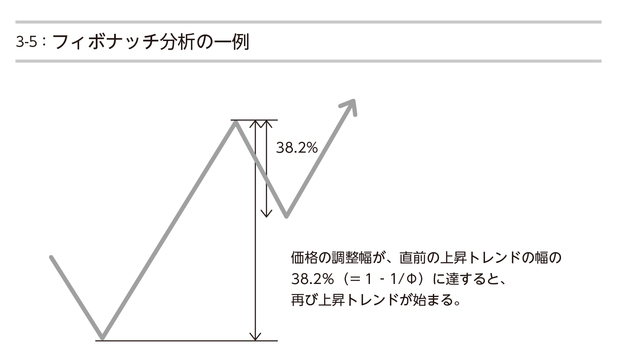
 実は、黄金律もフィボナッチ数も、チャート分析では好んで使われるものだ。そこには、ピタゴラスのような「数の中には万物の秩序が秘められている」という感覚が反映されている。実際の相場変動でも、フィボナッチ数や黄金律が、相場の周期や値動きの幅に見いだされることがしばしばある。あるトレンドがスタートしてから144日（144はフィボナッチ数である）経つとトレンドが転換するとか、上昇トレンドがいったん途絶えて、その値上がり幅の38％（＝1－1÷Φ）分価格が下がったところで、相場上昇が再開する（図3－5）というようなことだ。もちろん、そうならないケースもあるのだが、ぴたりと当てはまっているケースに出くわすと、とても神秘的な気持ちになる。チャート分析を極めれば極めるほど、こうした数の神秘に引き付けられていく。

 実は、これがチャート分析のもう1つの落とし穴だ。神秘的な数的秩序が何を表すものなのかはわからない。だが、その神秘的な数的秩序によって相場の予測が可能になるという考え方には明らかに飛躍がある。神秘を極めることで必勝法が見つかるはずだというのは、一種の宗教といっていい。

 チャート分析の専門家が、こうした世界にはまっていくのは、実際によくあることだ。占星術とチャート分析が融合するようなケースもある。それによって何が得られるのかは私にはわからないが、少なくとも多くの投資家にとって、こうした宗教的チャート分析は、市場の予測不能性という事実から目を背けさせることにしかつながらないとは言えるだろう。

 こうしたチャート分析の落とし穴には多くの金融のプロフェッショナルが気づいていて、そのために「自分は、チャート分析は一切しない」という立場をとる専門家もいる。彼らに言わせれば、チャート分析はオカルトまがいの似非科学ということになる。チャート分析の魅力にはまっていない一般の投資家のなかでも、そう考える人は少なくないだろう。

 それでは「チャートはオカルトである」という考え方には落とし穴がないのだろうか。次はそれを考えてみることにしよう。