ビジネスパーソンの必須スキルである数学を、一からおさらいする「学び直し!ビジネス数学」特集(全8回)。第2~6回では、中学&高校で学んだ数学を復習しつつ、それらが社会の中でどのように役立っているのか豊富な事例を紹介する。今回のテーマは1次関数・2次関数。そもそも、「関数」とは一体何だろうか。現役エンジニアで『数学大百科事典』の著者の蔵本貴文氏と、大人のための数学教室和の川原祐哉講師に、徹底解説してもらった。(「週刊ダイヤモンド」2019年2月9日号を基に再編集)
関数は「答えが出てくる箱」
数学の世界でしか見掛けない言葉といえば、「関数」だ。中学校の授業で初めて出くわしたときには違和感を覚えたものの、なんとなく慣れてしまった人が大半だろう。
それでは、関数とはいったい何か。あらためて聞かれると、答えに困ってしまうのではないだろうか。数学でつまずいた原因は関数だったという人は意外と多い。
そんな関数について、蔵本貴文氏は「数字を入れると答えの数字が出てくる箱のようなものと考えればいい」と説明する。
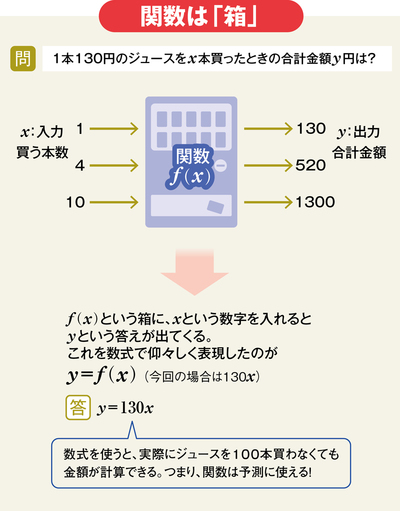
まずは、簡単な例から始めてみよう。1本130円のジュースを何本か買いたい。合計金額はいったい幾らになるのか。
買う本数が決まれば、合計金額は一つに決まる。1本買ったときは130円。4本の場合は520円。10本だと1300円になる。
買う本数という数字を入れれば、合計金額という答えの数字が出てくる。これが関数だ。
これを数学っぽく書くと、xが入れる数(買う本数)、yが出てくる数(合計金額)、f(x)が本数を金額に換えてくれる関数の箱(この場合は130x)になる。
ちなみに一部の数学者は、関数ではなく「函数」という書き方を好む。函には「箱」という意味があるため、数字を入れると答えが出てくる箱というイメージにはこちらの方がしっくりくる。
この例は簡単なので実感しづらいかもしれないが、関数のメリットは、「できないことでも確かめられる」点にある。
例えば、前述のジュースの例ならば、本当に100本買わなくても、合計金額は1万3000円になると知ることができる。太陽の位置を示す関数に1年後の日付を入れれば、1年たたなくても太陽の位置が分かる。
直接は見えない未来の姿を知るために、関数は発展してきたのだ。
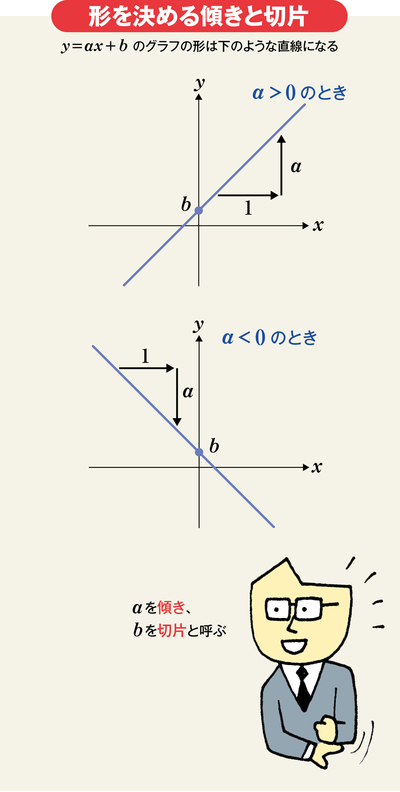
この関数のうち、最も単純なものが1次関数だ。y=ax+bという形で書くことができる。
1次関数で重要なのはこのaの部分で、「傾き」と呼ばれる。この意味は、xが1増えたときに、yがどれだけ増減したかだ。
グラフで描くと、aがプラスのときは右上がり、aがマイナスのときは右下がりの直線になる。傾きは第5回(9月12日公開予定)で説明する微分でも登場するので理解しておきたい。
また、bは、グラフがy軸と交わった場所のyの値で、「切片」と呼ばれる。
直線の特徴を決定づける
傾きと切片
1次関数の問題では、傾きと切片が問われることが多い。というのも、傾きと切片は、1次関数の直線の特徴を決定づける2大要素だからだ。
傾きと切片の意味を再確認するために、実際にありそうな身近な事例から考えてみよう。
年賀状の印刷を、次の二つの店のどちらに発注するかを決めたい。
A店は年賀状5枚の印刷を発注すると2000円、15枚だと4000円掛かる(1枚当たりの値段は一定だとする)。
一方、B店は、初期費用として2000円掛かり、1枚150円で印刷をしてくれる。さて、A店とB店、いったいどちらの店に発注した方がお得なのか。
5枚のときはA店の方が安いことはすぐに分かるが、枚数が多いときはなんとなくB店の方がお得なような気がする。数字を眺めているだけだと、こうした漠然とした答えになりがちだ。
だが、1次関数のグラフを使うことで、この問題の答えがはっきり分かる。