ビジネスパーソンの必須スキルである数学を、一からおさらいする「学び直し!ビジネス数学」特集(全8回)。第2~6回では、中学&高校で学んだ数学を復習しつつ、それらが社会の中でどのように役立っているのか豊富な事例を紹介する。今回のテーマは三角関数と数列。いずれも、身近な生活の中に多くの利用例が隠れている。引き続き、現役エンジニアで『数学大百科事典』の著者の蔵本貴文氏と、大人のための数学教室和の川原祐哉講師に、徹底解説してもらった。(「週刊ダイヤモンド」2019年2月9日号を基に再編集)
三角関数は近代文明の土台
「サイン・コサインなんて、社会に出ると何の役にも立たない」
高校の数学で不要なものとして、なぜかやり玉に挙げられることの多い三角関数。1月にも橋下徹・元大阪府知事が、「三角関数なんて大人になってから使ったことがない。人生に必要な知識ではなく、全員が学ぶべきものではない」という趣旨の発言をして、物議を醸した。
この主張の是非はともかく、役に立つかどうかという観点で言えば、三角関数は近代文明の土台を陰で支える働き者だ。
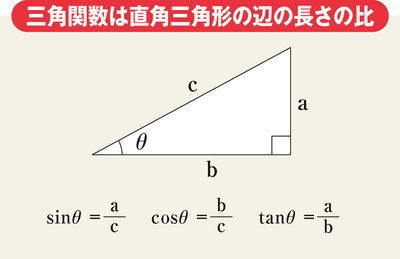
三角関数の基本は直角三角形だ。辺の長さの比、つまり、辺の長さの割り算で求められる。
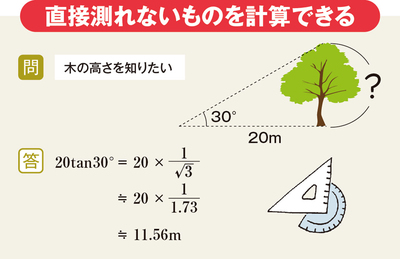
これを使う利点は、直接測れないものでも計算できることだ。例えば、木からの距離と、木のてっぺんとの角度が分かれば、木に登らなくても高さを計算できる。
約2600年前、ギリシャの哲学者タレスがピラミッドの高さを計算し、エジプトの王様の度肝を抜いたことが、三角関数の始まりだといわれている。
だが、直角三角形で考えていると、角度が90度のときまでしか使えない。この便利な道具を「もっと角度が大きいときにも使いたい」と、数学者たちは考えた。
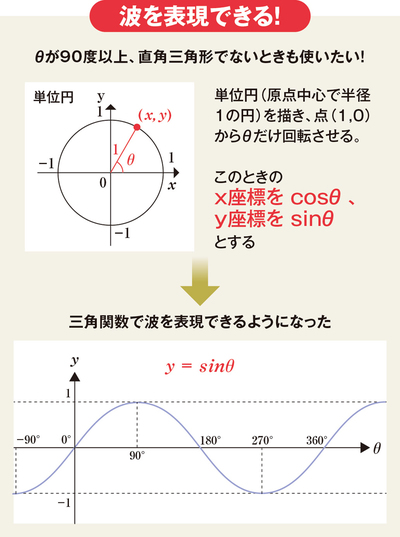
まず、半径1の円を描く。そして、円の右端から反時計回りにθの角度だけ回転させたときのx座標をcosθ、y座標をsinθにしようと決めた。
つまり、三角関数は円周上をぐるぐる回る点の位置を示すものなのだ。こうすることで、三角関数の可能性が爆発的に広がった。
横軸を角度、縦軸をsinθとしたグラフを見てみよう。sinθの値は0からだんだん増えていき、90度のときに最大の1となる。そこからは減っていき、270度で最小のマイナス1に、そして360度になると1周して0に戻る。
ここで登場したグラフの形は、波だ。その名前から直角三角形の印象が強い三角関数だが、その本質は、波を数式で表すことができるという点にある。
三角関数は波を表現できるようになったことで、あらゆる波を操る魔法の道具へと化けた。
電気や音といった「波」を制御できる
私たちの身の回りは、波であふれている。電気や音、電波や光は全て波だ。三角関数を使うことで、こうした波を機械が理解できる数学の言葉を使って制御できるようになったのだ。
だから、三角関数がなければ、家電は動かないし、スピーカーから音楽は流れず、スマートフォンの通話もできなくなるのだ。
実際、コンセントの交流電源は三角関数の式で表現できる。下図は東日本の場合だが、1秒間に50回、波の上下を繰り返すので周波数は50ヘルツ(Hz)と呼ぶ。
西日本は60ヘルツと周波数が違うので、東日本の家電が使えないという話を聞いた人も多いだろう。
波を制御できると、情報も波を使って届けられるようになる。その代表例が、ラジオだ。
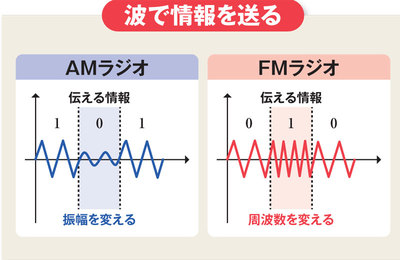
電波に情報を乗せる方法は、大きく2通りある。波の高さ(振幅)を信号にする方法と、周波数を信号にする方法だ。
どちらの手法も現実に使われており、AMラジオでは振幅を変えることで情報を送っており、FMラジオでは周波数を変える方式を使っている。
また、高校時代に、加法定理や積和の公式といった複雑な式の暗記に悩まされた人も多いはずだ。だがこの式も、実はスマホの通信基盤を支えている。