
ビジネスパーソンの必須スキルである数学を、一からおさらいする「学び直し!ビジネス数学」特集(全8回)。最終回となる今回は、世界を変えた「数学史に残る方程式」ベスト7を紹介しよう。今日の経済社会を陰で支え、基礎を成している数学。人類の経済社会の発展の陰には、常に天才たちによる数学の発明があった。「サイエンスZERO」などでおなじみの竹内薫氏がナビゲートする。(「週刊ダイヤモンド」2016年1月23日号を基に再編集)
数学と世界の変化はドミノ倒し
世界が変わるというのは、要するに経済社会が変わるということである(ダイヤモンドの読者にとっては、当たり前の話だ)。では、経済社会が変わるとはどういうことか? それは、数学が進歩するということである。
ちょっと分かりにくいですか? ええと、数学が進歩すると、科学革命や産業革命が起こる。そして、産業革命が起こると経済社会が大きく変貌を遂げる、ということだ。
経済という建物の土台(基礎)に産業があり、産業の基礎に科学があり、科学を記述する言語が数学なのだといえば分かっていただけるだろうか。まるでドミノ倒しが広がるように、数学が進歩すると世界が変わるのである。
さて、前置きはこれくらいにして、早速、竹内薫が選ぶ方程式ベスト7を見ていこう。
方程式(1) ピタゴラスの定理
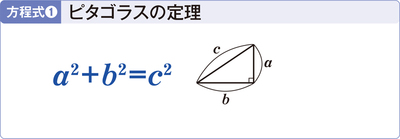
誰でも小学校で教わる方程式だが、この方程式こそは「三角測量」の基礎である。地上での測量術だけでなく、海上での航海技術にも欠かせない。実際、ピタゴラスの定理が存在しなかったら、人類は大海原を越えることができず、大航海時代もなかったに違いない。簡単な方程式だが、その威力は絶大だ。
方程式(2) 虚数

想像上の数などといわれ、数学が苦手な人がつまずくことの多い虚数。確かに、2乗しているのにマイナスになるなんて、非常識極まりない気もする。だが、虚数は、3次方程式の解の公式に(必然的に)出てきてしまうので、もし、虚数が存在しなかったら、人類は2次方程式までしか解けないという、かなり情けないことになってしまう。
ちなみに、学校では、2次方程式の解の公式までしか教わらないが、3次方程式や4次方程式の解の公式というのも存在する。だが……ここが数学の面白いところなのだが、なんと、5次方程式(より次数の高い方程式)には解の公式が存在しないのである! ご存じでしたか?
あと、虚数は、現代物理学の基礎になっている量子力学の方程式にも不可欠な存在だ。原子や素粒子、さらにはエレクトロニクスなどとも深く関係する量子力学だが、今では量子コンピュータなる、スーパーコンピュータを凌駕するコンピュータも登場しつつある。虚数がなかったら、人類はどうなっていただろうか。考えるだけでも恐ろしい。
方程式(3) 微分積分

これも数学嫌いの人が特に嫌う数学分野だろう。数式をご覧いただくと分かるように、やっていることは引き算と割り算と極限操作だけだ。しかし、この極限操作が意外と曲者(くせもの)。
例えば、0.9、0.99、0.999という具合に下から1に近づいていって、その極限の0.9999999……(9が無限に続く)が1だと言われても、「でも、それはホンモノの1とはちょっと違うのではないか?」という素朴な疑問が払拭できない。だが、数学が得意な人は、この気持ち悪さに論理的に立ち向かう。下から無限に近づいても到達しないのではないかと心配ならば、逆に上から近づいてみればいいのだ。1.1、1.01、1.001、1.0000000……と上からも押さえてみれば、1を上下からサンドイッチする恰好になる。上と下から無限に近づいてきたら、どう考えたって、最終的に真ん中に取り残される数は「1」以外にないではないか!
 アイザック・ニュートン(1642~1727)。微分積分学の発展に貢献。Photo:アフロ
アイザック・ニュートン(1642~1727)。微分積分学の発展に貢献。Photo:アフロ
ところで、この微分積分、いったいどのように世界を変えたのか? ちょっと理解しにくいのだが、無限に小さな変化を扱うことができるようになったおかげで、数学や物理学が飛躍的に進歩したのだ。例えば、距離を微分すると速度になり、速度を微分すると加速度になる。そういった計算の基礎には常に微分積分がある。
この後に出てくるマクスウェルの方程式やブラック=ショールズ方程式は「偏微分」方程式といわれるものだが、もちろん、微分積分が存在しなければ、これらの方程式も存在しない。
まあ、無限小を扱うために、その御利益(ごりやく)も見えにくいけれど、なくなってしまったら世界がひっくり返るような存在だとご理解いただければと思う。
方程式(4) マクスウェルの方程式

知る人ぞ知る、ジェイムズ・クラーク・マクスウェルといえば、アイザック・ニュートンやアルベルト・アインシュタインと並ぶほどの天才物理学者だ。ニュートンが力学の諸法則をまとめ上げたのと同じように、マクスウェルは電磁気学の諸法則をまとめた。アンペールの法則、ガウスの法則、ファラデーの法則、そして磁束保存の法則。
マクスウェルは、単に先人の業績をまとめただけでなく、一つの独創を方程式に盛り込んだ。それは方程式の中のたった一つの「つなぎ」みたいな数式(∂D/∂t)なのだが、この工夫によって、人類の文明が大きく開化することとなった。実は、マクスウェルのおかげで、人類は「電波」が使えるようになったのだ。
マクスウェルの方程式を少しいじくると、空間を波として伝わる「電磁波」を表す部分が出てくる。この数学的な予言を基に、1888年、ハインリッヒ・ヘルツが電磁波を実験的に検証して、現在の携帯電話やWi-Fi(ワイファイ)、GPSといった電波社会への道が開かれたのだ。
ちなみに、ファラデーの法則で知られるマイケル・ファラデーと、時の財務大臣グラッドストーンとの会話が、いまだに科学界では語り草になっている。
「今のは素晴らしい実験だったが、いったい何の役に立つのかね?」(グラッドストーン)
「何の役に立つかは分かりませんが、将来、閣下はこの発見に税金を課すことになるでしょう」(ファラデー)
実は、ファラデーの法則こそは、現代のモーターと発電機の原理そのものなのだ。発見時には、何の役に立つのかが分からない。でも、100年たつと、その方程式は、文字通り世界を変える。
電波通信、モーター、発電機……マクスウェルの方程式が生み出した経済効果を真面目に計算したら、途方もない金額になることだろう。







