ビジネスパーソンの必須スキルである数学を、一からおさらいする「学び直し!ビジネス数学」特集(全8回)。第2~6回では、中学&高校で学んだ数学を復習しつつ、それらが社会の中でどのように役立っているのか豊富な事例を紹介する。学び直しの最後となる第6回のテーマはベクトル。データ分析に欠かせないベクトルは、ビジネスの鍵を握る重要ツールでもある。データサイエンティスト、堅田洋資・データミックス代表取締役による講義を基に、その基礎を解説しよう。(「週刊ダイヤモンド」2018年6月30日号を基に再編集)
ベクトルは「大きさと向きのある量」
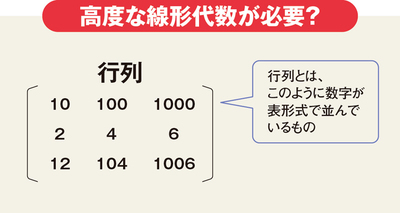
文系ビジネスマンにとっては、ベクトルと行列もまたとっつきにくいもの。ただ、高度な線形代数といった難しいことを考える必要はない。まず、数字が表の形で並んでいるものが行列である、と考えればいい。
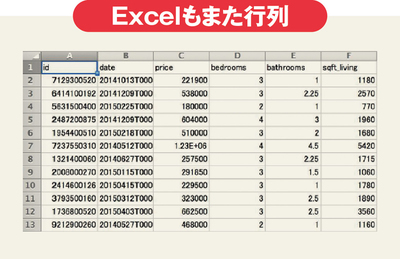
よく使われるExcel(エクセル)。これも行列だ。画像のデータもそう。写真を撮るということは、行列を作っているということでもある。
チャットボットが注目を集めているが、これも文書のデータを分析するために、単語にばらしてから表にしている。
ソーシャル・ネットワーキング・サービスの中の関係性のような、もやっとしたものを分析するときもしかり。Aさん、Bさん、Cさんのうち、誰と誰の仲がいいかを分析するには、例えば、それぞれがメッセージをやりとりした回数を表に置き換えたりする。
データ分析では、何でもかんでも行列にするのだ。だが、行列の扱いを学んでいく前に必要となるのが、ベクトルについての理解だ。
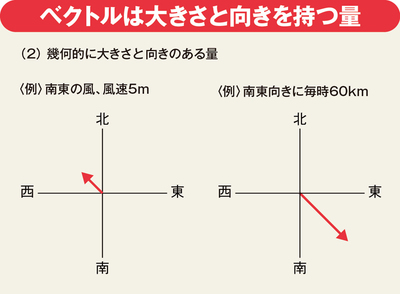
ベクトルとは何か。平たく言えば、一覧表のような行列に対して、縦(行)や横(列)1列に数字を並べたものだ。ただ、この理解だとデータ分析で使うにはいまひとつ。ベクトルとは「幾何学的に大きさと向きのある量」だと考えてほしい。
「南東の風、風速5メートル」がベクトル的表現であるように、ベクトルとは矢印。数字が並んでいるものはベクトル、ベクトルを見たら矢印だと思うことだ。
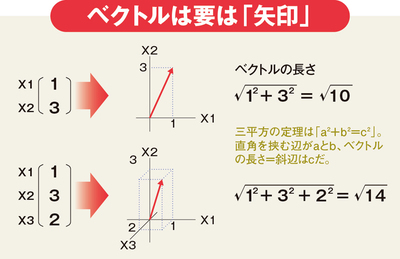
次の図を見てほしい。横に1、縦に3という矢印がある。矢印だから当然長さがある。
中学校で習った「三平方の定理」を覚えているだろうか?
a2+b2=c2 (aとbは直角三角形の直角を挟む2辺の長さ、cは斜辺の長さ)
これを使うと、矢印の長さは、横軸1の2乗と縦軸3の2乗を足してルートを取り、√10になる。ルートは平方根のことだ。4は2×2なので、√4は2となる。
こうしたベクトルは、足し算も引き算もできる。定数を掛けることもできる。だが、この理解だけではダメだ。
次の図をじっくりと見てほしい。
図の式を機械的に解くなら、
2×1+3×3=11
2×3+3×7=27
このように計算すればいい。だが、解くことは簡単だが、その意味を図形的に理解したい。
図において、横1、縦3の青の矢印に2を掛けることは、2倍に伸ばして赤の矢印にすることだと考える。つまり、横2、縦6の矢印になるということだ。同じく横3、縦7の矢印を3倍に伸ばせば、横9、縦21の緑の矢印になる。
さらに、この赤の矢印と緑の矢印と足すということは、途中でつなげることだと捉えるのだ。すると、つなげてできる矢印は橙色の矢印となることがわかるだろう。