
ビジネスパーソンの必須スキルである数学を、一からおさらいする「学び直し!ビジネス数学」特集(全8回)。第7回は、超難関で知られる東京大学の数学の過去問から、「数学のセンス」とは何かについて学んでいこう。東大入試と聞くと「難問だ」と身構えるかもしれないが、実は奇をてらった問題は少なく、むしろ数学のセンスや基礎学力を身に付ける格好の教材だ。そんな“伝説の良問”を、河合塾の大竹真一講師に解説してもらった。(「週刊ダイヤモンド」2018年6月30日号を基に再編集)
東大入試に求められる「数学のセンス」とは?
「数学のセンス」とはいったい何でしょうか。「計算が速い」だけでは、どうも違う気がします。「公式をよく知っている」というのもちょっと違うかな。でも、「公式を自由に使うことができる」となるとセンスかなあ、と感じるかもしれません。
そこで、東京大学の入試問題を見てみましょう。どのようなセンスや基礎学力が要求されているかを念頭に置きながら、問題を楽しんでください。数学を楽しむことができる。これも重要な数学のセンスでしょうね。
伝説の良問 1
円周率を計算!?

円周率πは古代ギリシャから今日に至るまで、さまざまな話題を提供してくれる数です。
3.14159……と延々と(周期性がなく)続く超越数であるという難しさと、円周の長さとその円の直径の比という小学生でも分かる身近さの、二つの顔を持つ点が人気の秘密なのでしょう。
このようなすてきな数は、他には見当たりません。このすてきな数を東大は入試問題にしました。でも、円周率が3.14ではなく、3.05より大? なぜでしょうか。
約2200年前、ギリシャのアルキメデスは、円に内接する正96角形と円に外接する正96角形の周の長さを計算して比較し、πは71分の233と7分の22の間にあることを見つけました。πの値が直接求められないならば、πに近づく方法を考えればよいという現代の解析学に近いような考え方をすでにしていたのです。
日本でも、江戸時代の数学者、建部賢弘(たけべ・かたひろ)が正方形から始め、加速法という手法を駆使して正1024角形までを計算し、小数点以下41桁まで求めたといいます。
この東西二つの計算法は、円周率を円周の長さと直径の関係で捉え、正多角形を用いるという、基本的には同じ考え方ですね。
話はちょっと脱線しますが、ここに東西の文化の違いが隠れています。アルキメデスの正96角形の96は6の16倍ですから、まず正六角形からスタートし、正12角形、正24角形……と次々に辺の数を2倍にして計算したのです。
一方、1024は2の10乗ですから、建部は正方形からスタートし、正八角形、正16角形、……正512角形、正1024角形と2倍にして計算していったようです。
西洋のアルキメデスは合理的で、1辺の長さが半径に等しい正六角形から始めたのですが、建部のスタートは正方形。日本は木の文化で、門などの造形の基調は四角形であり、西洋のようなアーチは少ないので、正方形から始める方が自然だったのかもしれませんね。
さて、東大入試はまさしくこれらの方法でπを求めなさいという趣旨でしょう。まず正六角形ならば、周の長さは半径の6倍。円周率は「3より大」と求められますが、東大の要求は「3.05より大」を示すことですから、惜しい!
ならば、正六角形の次に正八角形を調べようという人と、正12角形を調べようという人がいるでしょう。いずれの方法も3.05より大きいと示すことができます。3.14に比べて、かなり大まかな近似値ですから、OKとなるわけですね。これが、東大が3.05に込めた秘密なのです。
この計算は小学生でもできます。半径が1の円に内接する正六角形と正12角形を描き、考察してみましょう。
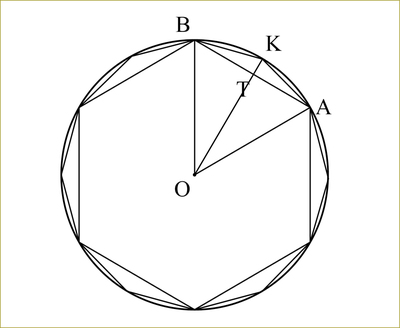
図で、三角形OATは正三角形の半分の直角三角形。
OA=1、AT=0.5だから、三平方の定理(ピタゴラスの定理)により、OTの長さが分かります。OK=1から、KTの長さが計算でき、さらに、直角三角形KTAに三平方の定理を用いてAK、つまり正12角形の1辺の長さを得ることができます。概算は次の図のようになります。
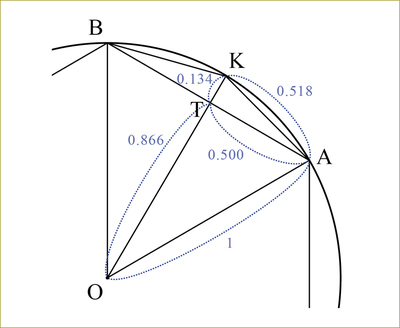
正12角形の周の長さは、0.518×12=6.216。円周の長さ2πはこれよりも大きいので、πは3.108よりも大きい。これで東大はほぼ合格ですね。
このように、東大はπの近似値を求める計算方法を自ら見いだして計算できるかを問うているのですね。単に計算するだけでなく、その方法も見いだす。これが本当の意味での計算力です。計算のセンスを垣間見ることができる良問でしょう。







