ビジネスパーソンの必須スキルである数学を、一からおさらいする「学び直し!ビジネス数学」特集(全8回)。第2~6回では、中学&高校で学んだ数学を復習しつつ、それらが社会の中でどのように役立っているのか豊富な事例を紹介する。今回のテーマは微分・積分。学生時代にこの辺りからつまずいたという人も多いだろうが、構える必要はない。引き続き、現役エンジニアで『数学大百科事典』の著者の蔵本貴文氏と、大人のための数学教室和の川原祐哉講師に、分かりやすく解説してもらった。(「週刊ダイヤモンド」2019年2月9日号を基に再編集)
面積を計算するのが「積分」
微積分とセットで扱われることも多い微分と積分。でも、“積微分”と呼ばれることはなく、前に出てくるのはいつも微分だ。高校の授業でも、学ぶのは微分が先だ。
これは「極限」→「微分」→「積分」という順に学んだ方が数学的に厳密、つまり、数学者にとって“美しい”からだ。しかし、普通の人が概念をざっくりつかみたいならば、「積分を先に学んだ方が分かりやすい」(蔵本貴文氏)。
というのも、積分の考え方が登場して使われ始めたのは紀元前。一方、微分が本格的に実用化されたのは1600年代になってから。つまり、積分の方が先に見つかった考え方であり、簡単なのだ。
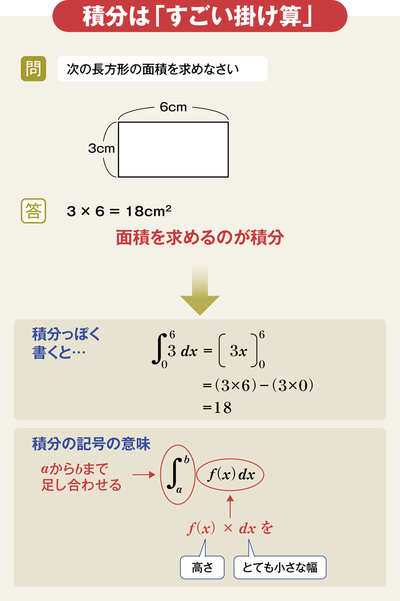
論より証拠。まず縦3cm、横6cmの長方形の面積を計算してみよう。答えは18cm2とすぐ分かる。この長方形の面積を求める計算が、実は積分だ。
「積分っぽく」書くと図のようになる。難しく見えるが、やっていることは高さ3の小さな幅の長方形を、0から6の範囲まで足しているだけだ。
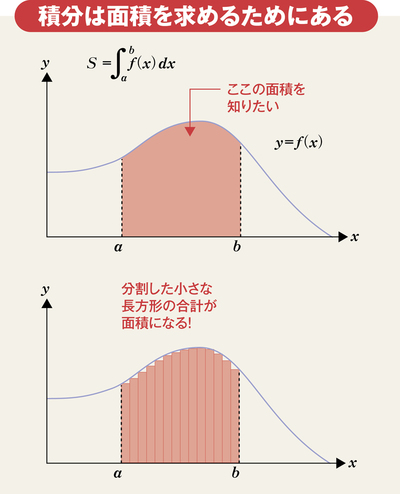
積分のメリットは、長方形のようなシンプルな形でなくとも、小さな幅の長方形を並べて足し合わせるという考え方をすれば、その面積が求められるところにある。つまり、積分はよく分からない形の面積を計算することができる、「すごい掛け算」なのだ。
積分を使う例の一つが、スマートフォンなどのバッテリー残量表示だ。昔は3段階表示も多かったが、今は1%単位で教えてくれる。
消費電力が一定ならば、残量の計算は簡単だ。だが、実際には頻繁に画面をつけたり消したりするし、動画の視聴やゲームなど、使う電気の量はコロコロ変わる。
そこで積分を使う。時間によって上下する電流の値を積分することで、その面積、つまり使った電気の量を計算することができ、バッテリー残量の推定が可能になるというわけだ。
DVDに株価、変化を読み取る「微分」
積分がすごい掛け算だとするならば、微分はその逆だ。「すごい割り算」だと考えればいい。
小学生の割り算の代表的な問題が速度の計算だ。2時間かけて60キロメートル進んだ車の速さは、60を2で割り、時速30キロメートルと計算できる。
高校生になると、設定が少し難しくなる。例えば、車のスピードが一定ではない場合で、1時間後の速さを知りたいとき、簡単な計算で求めることはできない。