天才数学者たちの知性の煌めき、絵画や音楽などの背景にある芸術性、ＡＩやビッグデータを支える有用性…。とても美しくて、あまりにも深遠で、ものすごく役に立つ学問である数学の魅力を、身近な話題を導入に、語りかけるような文章、丁寧な説明で解き明かす数学エッセイ『とてつもない数学』が6月4日に発刊。発売4日で1万部の大増刷、その後も増刷が続いている。
鎌田浩毅氏（京都大学教授）「数学“零点”を取った私のトラウマを払拭してくれた」（「プレジデント2020/9/4号」）、「人気の数学塾塾長が数学の奥深さと美しさ、社会への影響力などを数学愛たっぷりにつづる。読みやすく編集され、数学の扉が開くきっかけになるかもしれない」（朝日新聞2020/7/25掲載）、佐藤優氏「永野裕之著『とてつもない数学』は、粉飾決算を見抜く力を付ける上でも有効だ」（「週刊ダイヤモンド2020/7/18号」）、教育系YouTuberヨビノリたくみ氏「色々な角度から『数学の美しさ』を実感できる一冊!!」と絶賛されている。2020年のノーベル物理学賞に英国オックスフォード大学のロジャー・ペンローズ氏が選ばれた。優れた数学者でもあるペンローズ氏の受賞を祝福して著者が緊急寄稿した。連載のバックナンバーはこちらから。
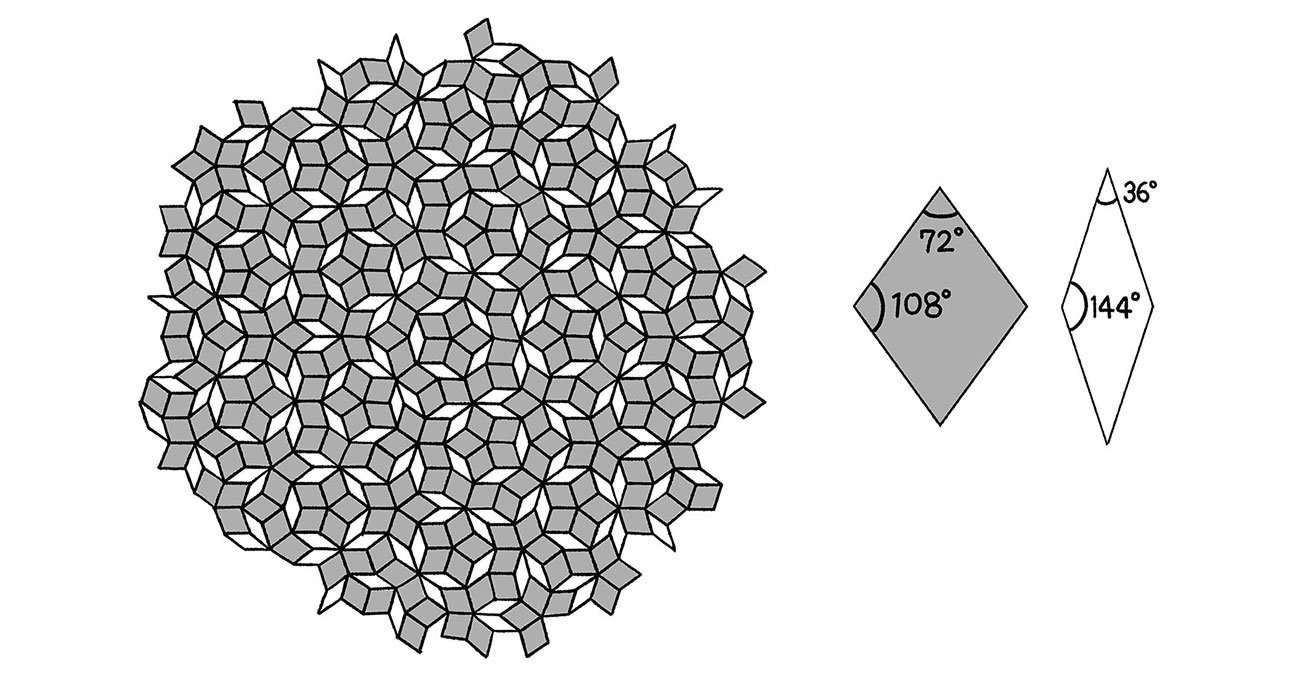【ペンローズ・タイル】 イラスト：ことり野デス子
2種類のひし形で平面を埋めつくす
数学の三大分野と言えば、方程式を扱う「代数学」、関数を扱う「解析学」、そして図形を扱う「幾何学」の3つを指す。
その幾何学の中で、紀元前1000年頃から研究が始まり、今もなお活発な議論が交わされている分野がある。タイリングとかテセレーションと呼ばれるもので、日本語では平面充填（じゅうてん）という。
街の歩道や建造物などに見られるタイル張りには様々な模様があり、どれも大変美しい。いわゆる「だまし絵」の第一人者であるオランダの画家・版画家のマウリッツ・エッシャー（1898～1972）も、タイル張りの「無限に続くパターン」に魅せられた一人である。エッシャーが40代以降、ユニークな敷き詰め模様を描くようになったのは、スペインのアルハンブラ宮殿で目にした見事なタイル張り装飾の数々に感化されたからだった。
ただし、タイル張りに使う図形は何でもいいというわけではない。無限に続く平面を同じ形のタイルで埋め尽くそうとするとき、どのような形であれば隙間や重なりが無いように敷き詰められるかを考える「平面充填問題」は、実はとても奥が深いのだ。
つい先日、2020年のノーベル物理学賞に選出されたイギリスのロジャー・ペンローズ（1931～）は、優れた物理学者であると同時に、この平面充填問題を語るときには外すことのできない数学者でもある。
ペンローズは理論物理学者として、スティーヴン・ホーキング（1942～2018）と共にブラックホールの「特異点定理」を研究した。そして、一般相対性理論から重力が無限大になる「特異点」、つまりブラックホールが存在することを証明し、これが今回のノーベル賞の主な受賞理由になった。
ペンローズは、いわゆる「不可能図形」の研究でも知られている。「ペンローズの三角形」とか「ペンローズの階段」と呼ばれる図をご覧になったことがあるだろうか。
それらの不可能図形は、一見ある立体の見取り図に見えるのだが、よく見るとそのような物体は現実にはあり得ないことがわかる（たとえば「ペンローズの階段」は、階段を登りきったところが階段の一番下につながっている）という不思議な図だ。
人間の感覚やもののリアリティについて一石を投じる不可能図形は、今では数学者だけでなく、哲学者や心理学者、そして美術家などにも興味を持たれていて、広い分野に影響を及ぼしている。
さらにペンローズは、1972年に「ペンローズ・タイル」を考案し「平面充填問題」においても大きな足跡を残した。ペンローズ・タイルとは、2種類のひし形をある法則にしたがって並べて平面を埋めつくしたもののことを言う。特筆すべきはその並びが周期的ではないという点である。ペンローズ・タイルには、ある部分をどのように平行移動しても、ぴったりとは重ならない他の部分が存在する。
ペンローズ・タイルに代表されるような周期的ではない平面充填法の多くは、主に20世紀に入ってから発見された。それまでは平面充填と言えば、長方形を使ったタイル張りのように、「模様全体を平行移動すると重なる」という特徴を持つものがほとんどだった。非周期的平面充填法を考案するためには、類まれなインスピレーションに加えて高度な近現代数学が必要なのだ。
数学が導いた真実は、思いもよらない形で応用されることがある。ペンローズ・タイルもその例にもれない。
1982年にイスラエルの化学者ダニエル・シュヒトマン（1941～）は周期的な構造を持たない合金を発見した。それまで結晶と言えば、周期的な構造を持つというのが「常識」だったので、発表当時シュヒトマンははげしい批判を受けてしまう。
しかし彼は、ペンローズ・タイルを理論的裏付けにすることで、非周期的な構造を持つ結晶的なもの（準結晶という）も存在し得ると断固主張した。その後「準結晶」が次々と発見されたことで、シュヒトマンの功績は認められ、2011年にはノーベル化学賞が贈られている。
ペンローズの幾何学における功績は、もののカタチについての鋭い洞察を与えるだけでなく、遊び心とともに数学のとてつもない可能性を教えてくれる。そんな氏のノーベル賞受賞を心からお祝いしたい。
（本原稿は『とてつもない数学』に掲載された内容に大幅な加筆を加えたものです）
