だが実際には、「替えるべき」というのが答えだ。実は、あなたが最初に選んだドアの後ろに自動車がある確率は33.33……%で、もう一方のドアの後ろに自動車がある確率は66.66……%なのだ。この問題と正解がアメリカの雑誌に初めて発表されると、数学の教授も含めた何千人という読者から、まちがっているとの苦情が押し寄せた。それくらい、見かけよりもずっと理解するのが難しい問題なのだ。
まだ開いていないふたつのドアで確率が半々でない理由を理解するには、100個のドアのうち99個がヤギ、たったひとつが景品の自動車という状況で同じことをするところを想像するのがいちばんわかりやすい。あなたが1番ドアを選んだあと、司会者がヤギのいる98個のドアを開け、あなたが最初に選んだドアと100番ドアだけを残したとしよう(図25を参照)。
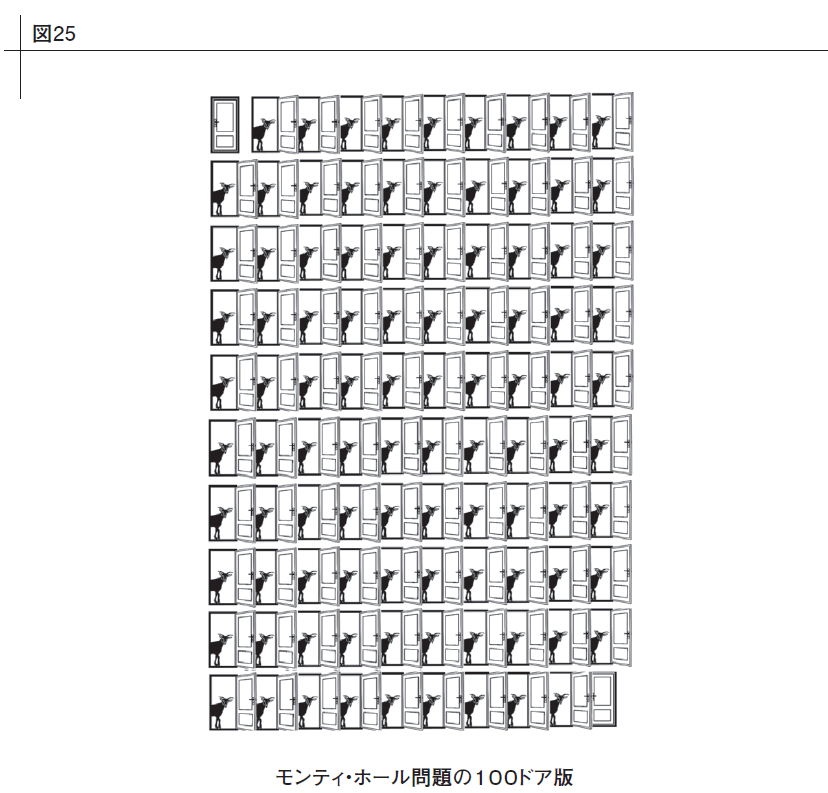
このバージョンなら、最初の選択が正しい確率はきっかり1%しかなく、もうひとつのドアのほうに自動車が隠れている確率は100分の99だということが簡単にわかるだろう。ほかの99個のドアのうち、はずれの98個を除外することで、司会者は残りのドアが正解だというほぼ確実な情報を自分から教えてくれたわけだ。選択を替えてはずれるのは、最初に選んだドアが奇跡的に正解だったケース、つまり100回に1回しかない。先ほどのドア3つのシナリオも理屈はまったく一緒だ。最初の選択が正しい確率は3分の1で変わっていないのだから、残ったドアが正しい確率は3分の2となり、選択を替えるべきなのである。