ランダムウォーク理論を前提としているファイナンスの世界では、株価だけでなく為替やオイル価格など、あらゆる相場にこの考え方が有効だとされている。実際の応用をイメージしていただくために、またモデルケースを考えてみよう。
X社の株価は現在100円である。この市場では1日に1円しか価格が変動しないとしよう。つまり、1円上がるか1円下がるかのどちらかしかないという前提だ。株価が10日連続で上がれば110円になるし、10日間下がり続ければ90円になる。もちろん、上がったり下がったりを繰り返した結果、10日後に100円近辺にいる可能性も十分ある。
まず1日が経過したとしよう。1円を得るか、1円を失うか、可能性は五分五分だ。
では2日目が終わった段階ではどうなるだろうか。2日とも上がってプラス2円となる可能性もあるし、2日とも下がるかもしれない。また、上昇と下落が1日ずつ起こり、損得は0という状態も考えられる。さらに、同様に3日後の可能性も考えてみよう。
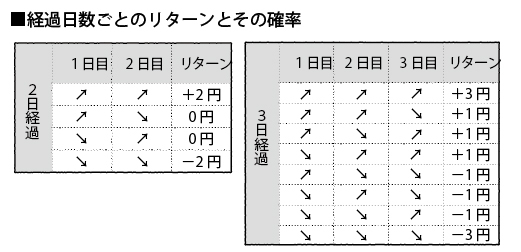
ここで重要なのは、日数を重ねるほどキャッシュのばらつきが大きくなるということだ。50日後には株価が50円(50日連続下落)になっているかもしれないし、150円(50日連続上昇)になっているかもしれない。当然、時間が経てば経つほど、不確実性は高まっていくように思える。
下の図を見ればわかるとおり、この取引における標準偏差は「経過日数の平方根」になっている。
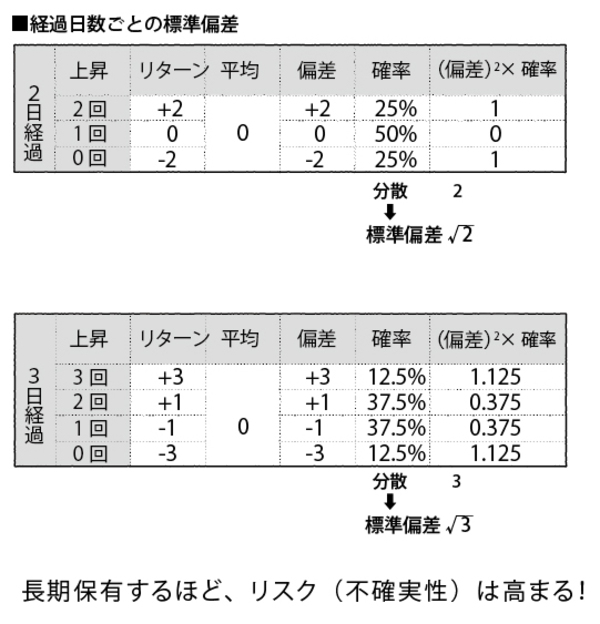
10日後の標準偏差は3.16円(10の平方根)、50日後は7.07円(50の平方根)である。これは端的に言えば、株式を長期間にわたって保有すればするほど、収益面でのリスクは増大するということだ。



