このように、ファイナンス理論では「標準偏差」と「期間の長さ」をもとに、相場のリスクを合理的に計算する。しかし、先述の例はあくまでもモデル化したケースであり、現実とは決定的に違う点がある。
それは「株価は0以下にならない」という事実だ。もしランダムウォークの結果、100日連続下がったとすると、株価は0円になってしまう。101日目に下落しようものなら、株価はマイナス1円となるが、現実にはこんなことはありえない。
株価の動きを1日1円という幅で考えると、このような不都合が出てくるため、ファイナンスの世界では資産価格の変動リスクも、百分率(%)で表すのが一般的だ。
100円から1%上昇すれば101円(=100×(1+0.01))、1%下落すれば99.0099円(=100÷(1+0.01))となる。
100円から100%上昇すれば200円(=100×(1+1))だし、100%下落すれば50円(=100÷(1+1))だ。
これを年率で表したものをボラティリティ(変動率)という。ある株のボラティリティが高いということは、株価のばらつきが大きい、つまり価格変動が激しいということを意味している。
たとえば、ある株がいま100円で取引されて、ボラティリティが100%のとき、その株は1年後には200円から50円の間に約3分の2(68.27%)の確率で収まっていることを意味するわけだ。
では、株価のボラティリティがどのように求められるのか、簡単に解説しよう。
Y社の株価が過去10日間、下図のような変動をしていたとする。
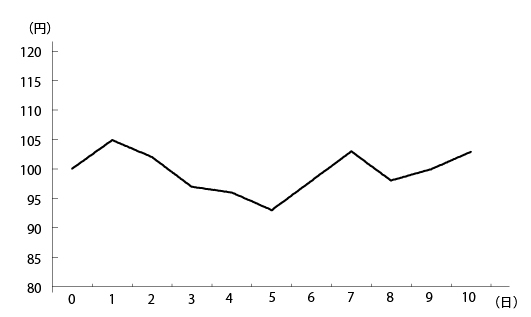
1日の変化は「その日の株価÷前日の株価」で求めることができる。1日目であれば105%(=105÷100)、2日目なら97.1%(=102÷105)である。変化率の平均100.4%をそれぞれの変化率から差し引いて偏差を割り出し、それぞれの2乗の平均値、すなわち分散を求める。分散は約0.16%となり、その平方根である標準偏差はおよそ「4」だ。
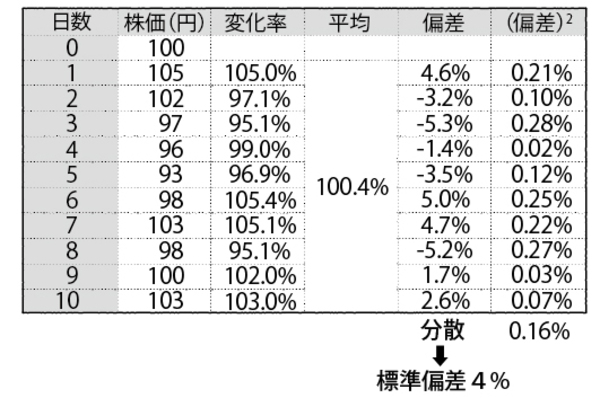
注意してほしいのは、ここで算出した株価の変動率の標準偏差は「1日分の変動」に過ぎないという点である。
ボラティリティは年率で表すことになっているので、1年間にこの株価がどれくらい変動するかを考えなければならない。休日を除いた暫定日数として1年を250日としよう。すでに147ページで見たとおり、リスクは「時間の平方根」に比例するので、250の平方根である15.8をかけ、今後1年間のボラティリティは62.75%(≒4×15.8)となる。
現在100円の株式Yのボラティリティ(変動率の標準偏差)が62.75%であるなら、1年後の株価は68.27%の確率で±62.75%の範囲に収まっている。つまり、約7割の確率で「61~163円くらいの幅」に収まっているだろうと予想できるわけだ。



