ここで相関効果の考え方を理解していただくため、次のような例を考えよう。あなたは手元資金100万円を2つの株式(IとJ)に分散投資することを検討しているとする。なお、リスクフリーレート(無リスク金利≒国際金利)は1%としておこう。それぞれの銘柄のリスク・リターンは次のとおり。
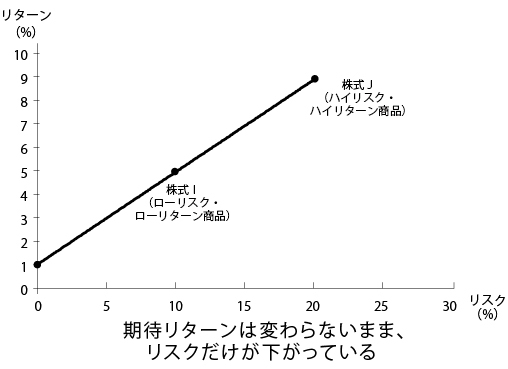
・株式I――リスク10%/期待リターン5%→ローリスク・ローリターン商品
・株式J――リスク20%/期待リターン9%→ハイリスク・ハイリターン商品
株式Iに100万円すべてを投資した場合と、株式Jに100万円すべてを投資した場合、両者のリスク・リターンが一直線上に並んで均衡を保っていることからもわかるとおり、どちらか一方に優劣はつけられない状況だ。
この仮想世界には好景気と不景気の2つしかなく、しかも、どちらかが50%の確率で起こる。
このとき、景気状況に応じてそれぞれの銘柄の期待リターンは、次のように変動するのだと仮定しよう。
・株式Iの期待リターン5%――[好景気]15%/[不景気]マイナス5%
・株式Jの期待リターン9%――[好景気]マイナス11%/[不景気]29%
さて、点Iと点Jを結ぶ線分IJに注目してみよう。これはIとJから構成されるポートフォリオの集合だと考えられそうだ。たとえば、線分IJのちょうど中間点は、Iに50万円、Jに50万円を投資したハイブリッド(混血)株式のリスク・リターンを表しているのではないだろうか。もしそうだとすれば、両者の平均値を割り出し、この投資のリスクは15%、期待リターンは7%になると言えそうだ。
しかし、驚くべきことにそうはならない。結論だけをいえば、リスクは5%、期待リターンは7%という結果になるのである。
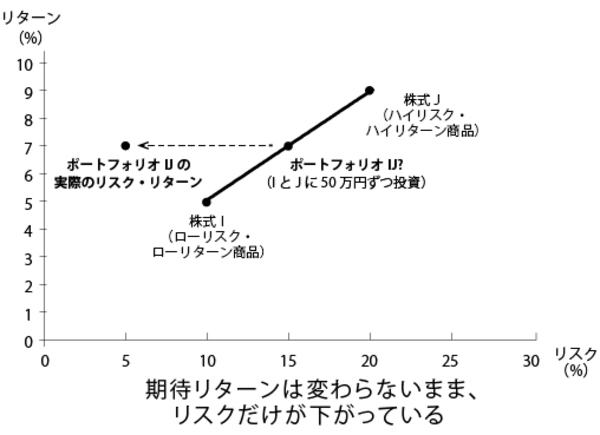
したがってポートフォリオIJのリスク・リターンは、線分IJよりも左にシフトすることになる。これが何を意味しているか、わかるだろうか?
そう、期待リターンは変わらないまま、リスクだけが下がっているのだ。
前回、僕たちは、「将来の稼ぎをキープしつつ、割引率だけを下げる方法はないか」という問いを立てた。IとJという2つの株式が存在する世界で、両者を半々の割合で購入するポートフォリオIJに投資するという行為は、まさにリターンを変えずに、リスクだけを小さくする道なのである。
なぜこんなことが起きるのだろうか?これこそがまさにポートフォリオの相関効果が功を奏した結果だ。
株式Iは、多くの株式と同様、景気がよければ利益が出て株価が上がり、不景気時には利益が減少して株価が下がる構造になっている。一方、株式Yは好景気のときは儲からないが、世の中が不景気なときほど儲かるという、何とも不思議な銘柄だ。
このように、正反対の動きをする銘柄を組み合わせることで、リターンはキープしつつ、両者のリスクをうまく相殺することができる。株式X・Yのようにまったく動きが逆になる銘柄はなかなか見つからないが、まったく同じ動きをするもの同士でない限り、必ず相関効果によるリスク低減は見込める。これがマーコウィッツの第2の発見だ。