Photo:PIXTA
Photo:PIXTA
2020年の入試も概ね終了に近づいている。そこで、人気校の算数の問題を振り返って、問題の傾向を見ていきたい。前回取り上げた全国一受験者の多い栄東に続き、長年入試問題を見続けてきた森上教育研究所「親のスキル研究会」講師である小板橋肇貴氏の解説を交えて見ていこう。(森上教育研究所)
例年より解きやすい問題が増えた
いまや千葉県を代表する進学校となった渋谷教育学園幕張(渋幕)。中学入試では県内に3校しかない2000人以上の志願者を集める人気校だ。
2月1日に一般入試が解禁される東京・神奈川の受験生が、併願校として腕試しに臨む姿も毎年恒例となっている。渋幕1回目(1月22日)の問題を例に、2020年の難関校の算数問題はどのような傾向だったのか見ていこう。なお、正解は最終ページにまとめて掲載した。
まず、今年の渋幕は、例年より解きやすい問題が増えたように感じる。大問は5つあるが、順に見ていくと、[1]規則性、[2]数の性質、[3]立体図形・水量変化、[4]平面図形、[5]立体図形、と各分野から出題されている。冒頭で解きやすいと申し上げたが、決して簡単な問題ではない。普段の学習の質が問われる問題にはなっている。
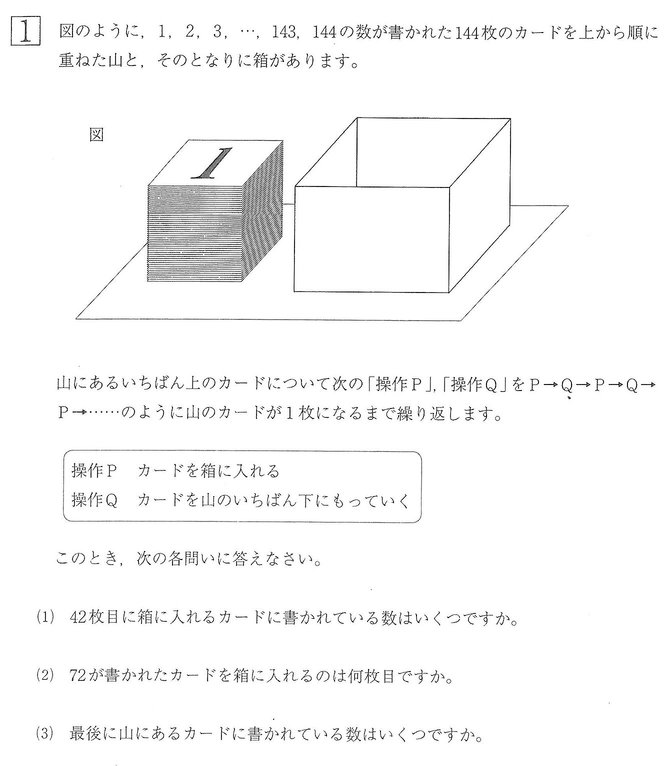
大問1は、継子だての一種類。室町時代から江戸時代にかけて行われた碁石を使う数学遊戯だ。渋幕を第一希望にしている生徒はもちろんのこと、塾によってはレギュラーの授業問題にあるので、解いたことがないということはないだろう。
次ページに載せたのが大問2。個人的にはこの問題がとても気に入っている。方陣算と連続する数の和というものを絡み合わせるとこういった問題になるのだろうなと思う。御三家と呼ばれる難関校の志望者は、連続する数の和は確実に解いておいてほしい問題ではある。とくに(3)は知識問題ともいえる問題ではないだろうか。