統計学と機械学習のための
数学ピラミッド

ビジネス書大賞（2014）、統計学会出版賞（2017）を受賞し、累計48万部を突破した大ヒットシリーズの最新刊、『統計学が最強の学問である［数学編］』が発売されました。今回は、統計学を支える数学がテーマです。

本書で提示される「統計学と機械学習を頂点とした数学教育のピラミッド」とは、どのようなものなのでしょうか？

統計学と機械学習を理解するのに、
幾何学の知識はほとんとど要らない

　高校までの数学カリキュラムを、理工系の専門家になるための微積分ではなく、統計学と機械学習への入門を頂点に設定してピラミッドを再編成した場合、学ぶべき内容を大幅に絞り込むことができます。

　なぜこのようなことが可能なのでしょうか？その理由をみなさんが理解するために、まずは現代の中等教育（中学校と高校）の数学カリキュラムがどのようなものから成り立っているかを説明しましょう。数学Iだとか数学Bだとかいった名前からはその実態があまり見えてきませんが、中等教育における数学カリキュラムは大きく、1）代数学、2）幾何学、3）解析学、4）確率・統計などを含む「その他の分野」、という4分野に分けることができます。

　これらの具体例を挙げてみましょう。数をxやyといった文字で表して計算しようというのは代数学にあたります。実際の「数」の「代」わりに文字や記号を使おうというわけです。一方、三角形や立方体の性質を考えるのは幾何学です。一定の規則性を持つ図形や模様のことを「幾何学的」と表現したりもしますね。また、微分や積分を行なうことは解析学にあたります。

　中学校でも高校でも、こうした分野が混在している状態で教わっていますが、当然ピラミッドの部品である「単元」について、代数学は代数学同士、幾何学は幾何学同士の関係性が強いことは言うまでもありません。そして統計学と機械学習を理解しようとする際、幾何学よりも代数学や解析学の方が圧倒的に重要になります。たとえば、円柱の体積や表面積を求められなくても、統計学と機械学習の勉強にはそれほど差し支えがありません。

なぜ人類は、長らく
確率や統計という概念を思いつけなかったのか？

　これは私が個人的にそう思っている、というわけではなく、きちんとした歴史的な経緯を説明することだってできます。

　カナダの科学哲学者であるイアン・ハッキングはその著書『確率の出現』の中で、なぜ人類は17世紀になるまで近代的な意味での確率や統計という概念を思いつけなかったのかについて論じました。

　サイコロとして使われていたと考えられる加工された動物の骨や、賭博の勝敗記録は古代エジプトの遺跡からも発掘されます。ユダヤ教の聖典にも「くじ」という言葉が登場します。また、ローマ皇帝のマルクス・アウレリウスはサイコロ賭博に熱中したと伝えられています。つまり、少なくとも有史以来人類はずっと、確率を使って遊んだり意思決定をしたりしていたということになります。

　そして、我々が中学校や高校で習うレベルの幾何学の知識は、古代ギリシャの時点ですでに発見されています。足し算や掛け算、分数といった概念が生まれた時代ともなれば、私には調べようもないくらい昔としか言いようがありません。しかしながら、近代的な確率論は、17世紀の数学者ブレーズ・パスカルらからはじまった、というのが学校でよく教えられる歴史です。古代のエジプトやローマ、ギリシャからなぜこれほど時間がかかったのでしょうか？

　この問いに対する説明の1つとしてハッキングは、「確率について考えようとすれば代数学など“数の表し方”の発展が不可欠だったから」という考え方を提示しました。代数学は幾何学と比べれば歴史は浅く、代数学（algebra）という単語の語源はアラビアの数学者であるフワーリズミーが9世紀に著した書物に由来しています。また、未知の数あるいは値が変わりうる数（後で詳しく述べますがこれを変数と呼びます）をxやyといった文字を使って表すようになったのは、フランスの哲学者/数学者であるルネ・デカルトが17世紀に著した、今日『方法序説』と呼ばれるテキストを含む長ったらしい名前の書籍からです。こうした便利な道具が揃ったことではじめて、人類は確率といった概念を理解して使いこなせるようになったのではないか、というのです。なお、英語で偶然という意味を持つchanceやhazardといった単語も、元を辿れば代数学（algebra）と同じくアラビア語が語源となっているそうです。

　イアン・ハッキングの本は「それだけでは十分な答えではない」というところから考察を深めていきますので、興味がある方はぜひご一読ください。ただ、確かに私たちが学生時代に習うような最低限の数学的な道具がなければ、確率や統計について考えることはとても難しくなります。

　そうしたわけで、本書で考える「統計学と機械学習のためのピラミッド」は、中高時代に習う代数学と解析学を中心とし、逆に中高時代の数学から、かなり大胆に幾何学の分野をカットしたものとしました。

　私なりに現行のカリキュラムをピラミッド状に整理すると、図表0-1に示すように、小学校ではまず平面図形（直線や三角形、円など）と立体図形（立方体や三角錐、球など）の性質を学びます。次に平行や合同、相似や比といった図形同士の関係性とそれに基づく証明方法を習います。その後、三平方の定理を学び、平面図形や立体図形を数式で表す方法を学び、最終的には数式で表された図形を積分して、面積や体積を求められるようになる、というのが1つのゴールになります。こうしたスキルは、機械の設計などエンジニアに必要な技術の基礎になるはずです。

　
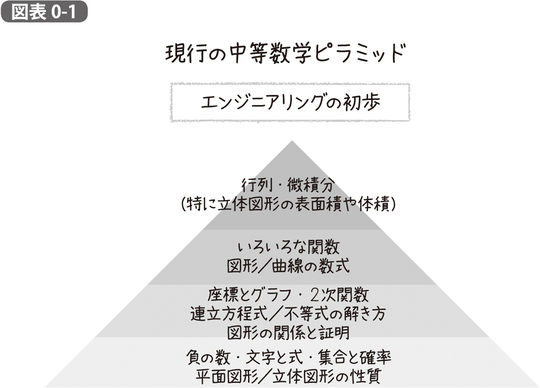
　しかし、本書の考える統計学と機械学習の基礎を理解するに足るカリキュラムでは、これらの内容をばっさりカットします。そのようなピラミッドを、図表0-2のように示すことができるでしょう。これらを下の層から順番にやっていく、というのがそのまま本書の章立てとなります。
 

 

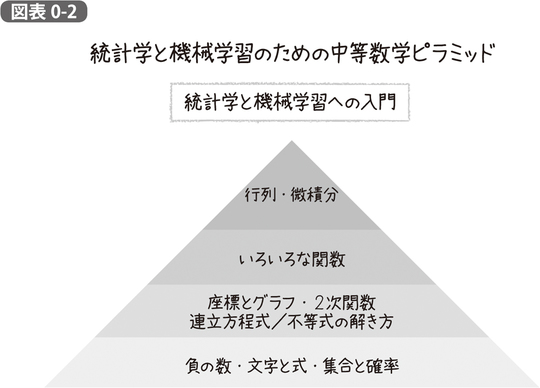
『統計学が最強の学問である［数学編］』の構成

　まず第1章では、xやyといった文字によって数を表すことにどんな意味とメリットがあるのかという、初歩的な代数学の考え方に入門します。ここで引き算や割り算といった小学校で習う計算についても、代数学的なお作法に則って使えるようになりましょう。ハッキングが提示した考え方に基づくと、これらの基本がわかっていることは確率を数学的に考えるためのだいじな素養になるはずです。せっかくですので第1章のしめくくりには、ベイズの定理という現代的な統計学と機械学習の中でもとても役立つ考え方を紹介しておきたいと思います。

　次に第2章では、知らない数が1つだけではなく、互いに関係し合うものが2つあった場合の扱いについて学んでいきます。座標とグラフによってどれだけ数同士の関係性がわかりやすく示せるのか、という考え方のほか、連立方程式や不等式を解くやり方についても説明しておきましょう。ここで扱うのは中高時代に習う基本的な1次関数や2次関数といったものだけですが、それだけでも統計学と機械学習の基礎にある「データとデータの間の最もあてはまりのよい数学的な関係性を推定する」という部分について理解することができます。この章の最後では、最小二乗法に基づく単回帰分析という、基本的な分析手法のことが理解できるようになります。

　第3章ではここからさらに発展して、指数、対数、三角関数といった、数同士のさまざまな関係性について学んでいきます。「幾何学を省く」という本書のコンセプト上、三角関数の内容は現行のカリキュラムと比べて大幅に削減されますが、それでも最低限、統計手法の理解に役立つところだけは説明しておきたいと思います。また指数と対数を理解することで、統計学におけるロジスティック回帰分析や、機械学習で使うシグモイド関数といったものがどのようなものかがわかることでしょう。

　そしていよいよ第4章と第5章では、それぞれ行列と微積分の話に入っていきます。こちらについても、3次元空間上の力の向きや回転を考えるとか、立体の体積を求めるといった幾何学的な計算は扱いません。それよりも、「データをまとめて記述する」とか「最もデータによく合う最適な値を選ぶ」といった、統計学と機械学習において重要な点に絞って説明したいと思います。

　第4章の最後には重回帰分析における「データとデータの関係」が、行列を使うとどうシンプルに表されるかを学びます。これは統計学と機械学習に共通して、専門書や論文を読む上でとても役に立つリテラシーとなるはずです。

　また、第5章の最後では、正規分布がなぜあのような数式で表されるのかという、多くの統計学の入門書であまり説明されていない部分について述べたいと思います。皆さんが今後、統計学の勉強をするにせよ、機械学習の勉強をするにせよ、これらの知識があれば変なところでつまづいてしまうリスクが減らせることでしょう。

　そして、最後の第6章では、行列と微積分を同時に扱います。統計学と機械学習に共通して、「データとデータの間の最もあてはまりのよい数学的な関係性を推定する」際には、行列を使って表された数式に対して、ベクトルで偏微分する、という考え方がよく出てきます。そうした数式を前にしても恐怖感やアレルギーを感じない、というのが本書の意図するゴールです。ここを最後まで読み通せば、大学レベルの統計学や機械学習の専門書などが、それほどストレスなく読みこなせるようになります。

　また、現代の「ITの統計学」あるいは「統計学の理論を応用した人工知能」の双方において、コンピューターは人間のように数式を解いて答えを出しているわけではなく、単純な繰り返し計算のアルゴリズムだけで複雑な微分の計算を行なっています。これが、「データとデータの間の最もあてはまりのよい数学的な関係性を推定する」という統計学と機械学習手法において大きな役割を果たしているわけですが、このような計算方法の基本についても本章では触れます。

　なお、代数学、解析学ともに、大学以降の数学の専門教育ではより広い概念として学びますが、本書で言う代数学とは「数を文字で表して整理する」という中高時代に習う基本的な考え方だけを扱います。また解析学も「微分したり積分したりする」という基本的な考え方だけを扱います。少なくとも以上のような内容を理解すれば、ディープラーニングなどの最近の人工知能技術も「よくわからないSF的な何か」などではないことがわかっていただけるはずです。