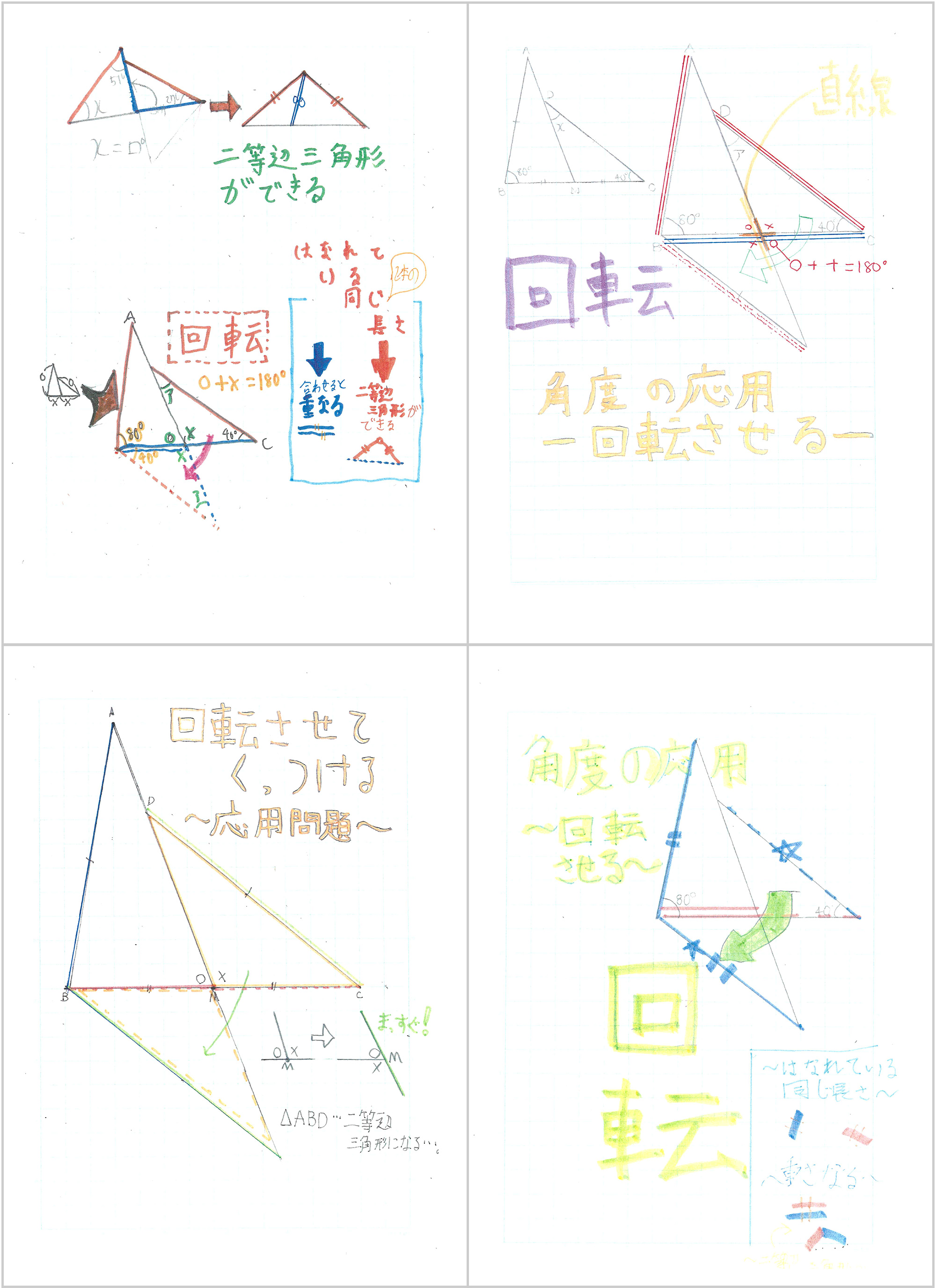
 角度を求める応用問題。図形を正しく描けているかどうかはノートを見れば分かる
角度を求める応用問題。図形を正しく描けているかどうかはノートを見れば分かる拡大画像表示
「図形」はセンスの問題か?
世の一般の生徒・親がイメージする図形感覚の有無は、持って生まれた音感、反射神経のたぐいで、簡単には変えられないというもののようだ。
小学校受験、いわゆるお受験を経験した生徒は、未就学児童のうちから図形に触れることで、図形に対するセンスを持ちやすいともいわれる。それでも、図が描ける、描けないという点では大きな差があると思う。
図を描く技術は、正しく描くという意識と習慣によって大きく変化する。正しい図を描くという意識を子どもが持つように、大人が教育しなければならないと思う。
実際の入試では、円やおうぎ形を描く場合、コンパスを使ってよい学校と、コンパスを使えない(フリーハンドで作図をする)学校とがある。子どもがコンパスを使う機会は塾ではなかなかないので、これは慣れさせておく必要がある。
また、フリーハンドで描く場合も、定規を使う場合も、正しく描かなければ描いたことにならないことを徹底させる必要がある。
漢字を書くとき、「口」を丸く書いたり、「木」をはねて書いてあっても、読めればよいという指導は教育ではない。
「直角」が直角ではなく、「平行」が平行ではなく、「等しい角」が等しくなく……という図を放置する指導も、教育ではない。
普通の塾では、生徒の描く図は放置される。
私の教室では、低学年(主に長さや面積を求める計算が始まる前の3年生)からフリーハンドとコンパスを使った両方の作図に時間をかけている。定規やコンパスでの作図は頭を使わない作業としてできてしまう側面もあるため、フリーハンドで、頭の中で図をイメージしながら描かせることを重視している。
最難関中学に合格した生徒たちの中にも、定規を使って「角が二等分されていない角の二等分線」を下の図のようにきれいに描く生徒が相当数いる。
小学生のときに教室で指導していなかった生徒が、中学生になって私の教室に合流する場合、合格すべくして東大や医大に合格していく生徒たちですら、ほとんどすべてがこのような図を定規で描いてしまう。
「だいたい等しいかな?」という感覚を持っていない、つまり、<正しい図形>というアンテナが欠如しているということになる。
小数や分数を学習した生徒は、円とおうぎ形の面積の問題を解けるようになる。そこで大切なことは、図を自分で描いて、その図を使って問題を解くという経験だ。
塾の授業やテストでは、<自分で図を描いて自分の図で解く>ということなしに、テキストの図に情報を書き込んで解くのが、たぶん普通である。
教室の生徒には、問題の図をよく観察して(円の中心がどこにあり、どのように描けば問題の図をコンパスで描くことができるかをよく考えて)コンパスでノートに書き、自分で描いた図で解くように指導する。
円とおうぎ形の問題には、普通5年生後半で習う相似がからまないので、4年生の間に、入試に登場する円とおうぎ形の最高レベルの問題まで解かせていく。
生徒たちは、相当集中して図を観察しないと、定規とコンパスで問題の図を正確に自分のノートに書き写すことができない。生徒たちは自然に、考えながら図を描くことを習慣化している。自分で図が描けるということは、円弧の中心がどこにあるかを見抜くからで、図を描きながら、その図の核心部分を把握し、図形の性質を見抜く練習を繰り返すことになる。
ご家庭で、塾ではやらない正しい図の描き方を身に付けるには、計算を伴わない図形の学習を低学年のうちから実行するのがよい。問題集にある図形を、フリーハンドと定規・コンパスで書き写す訓練をしておくことだ。
5年生、6年生の場合は、普段の塾の授業やテストでは自分で作図するような機会はほとんどない。だから、これはと思うようなてごわい大事な問題については、自分で図を描いて考えることを実行してほしい。
 今月、電子書籍で復活した『頭のいい子にも勝てる算数まとめノート』(ダイヤモンド社)
今月、電子書籍で復活した『頭のいい子にも勝てる算数まとめノート』(ダイヤモンド社)
今月、電子書籍で復活した『頭のいい子にも勝てる算数まとめノート』(ダイヤモンド社)の中には、私の教室で学んだ生徒の、実際のノートが多数収載されている。その数、文章題、規則性、図形(平面、立体)、場合の数、整数の250例に及んでいる。
ご覧いただくと一目瞭然だが、自分で描いて自分の図で解くという習慣が、誰にでも可能で必要な、図形問題が解けるようになるための条件といえる。
図形を学習することで、中高での数学の理解にも寄与する。社会に出てからも、立体的な感覚を持った思考力は、何かと役に立つ機会があるだろう。