天才数学者たちの知性の煌めき、絵画や音楽などの背景にある芸術性、AIやビッグデータを支える有用性…。とても美しくて、あまりにも深遠で、ものすごく役に立つ学問である数学の魅力を、身近な話題を導入に、語りかけるような文章、丁寧な説明で解き明かす数学エッセイ『とてつもない数学』が6月4日に発刊。発売4日で1万部の大増刷、その後も増刷が続いている。
鎌田浩毅氏(京都大学教授)「数学“零点”を取った私のトラウマを払拭してくれた」(「プレジデント2020/9/4号」)、「人気の数学塾塾長が数学の奥深さと美しさ、社会への影響力などを数学愛たっぷりにつづる。読みやすく編集され、数学の扉が開くきっかけになるかもしれない」(朝日新聞2020/7/25掲載)、佐藤優氏「永野裕之著『とてつもない数学』は、粉飾決算を見抜く力を付ける上でも有効だ」(「週刊ダイヤモンド2020/7/18号」)、教育系YouTuberヨビノリたくみ氏「色々な角度から『数学の美しさ』を実感できる一冊!!」と絶賛されたその内容の一部を紹介します。連載のバックナンバーはこちらから。
 Photo: Adobe Stock
Photo: Adobe Stock
東大入試の有名問題
「なぜ円周率は3.14なのだろう?」と考えたことはあるだろうか? かつて東京大学で「円周率が3.05より大きいことを証明しなさい」という問題が入試(2003年)に出たことがある。東大の数学の入試問題としてはおそらく最も有名な問題なので、ご存じの方もいるかもしれない。
そもそも円周率とはなんだろうか? 小学校のときに習った公式「直径×円周率=円周」を少し変形すれば、円周率とは(実は文字通りであるが)直径に対する円周の長さの割合だということがわかる。
円周の長さは直径の長さの3倍強というわけだ。言うまでもなく、すべての円は相似(同じ形)なので、このことはすべての円について成立する。ある円の円周は直径の3倍より短かったり、別の円の円周は直径の4倍だったりすることはない。逆に言えば、1つの円について、直径に対する円周の長さの割合を求めることができれば、それが円周率である。
アルキメデスはこう考えた
しかしながら「円周の長さ」を求めるのは簡単ではない。原始的な方法としては実際に測定するという手がある。たとえば、タイヤにペンキを塗っておいて(滑らないように)転がし、タイヤが1回転したときのペンキの跡の長さを測る。あるいは地面に杭を打って、そこにロープの一端を結び、別の端には先の尖った棒でも付けてコンパスのようなものを作り、円を描いた後、円周がロープの長さ(ロープは輪っかになっているので輪っかをほどけば、ロープの長さはほぼ直径に等しい)の何倍になっているかを測る。
実際、紀元前2000年頃のバビロニア地方(現在のイラク南部)では、後者の方法で「円周率」はおよそ3.125程度であると考えられていた。
とはいえ、測定には誤差がつきものである。測定に頼っている限り、なかなか正確な値はわからないであろう。そこで、古代ギリシャのアルキメデス(紀元前287?~紀元前212)は、正多角形を使って計算から円周の長さを見積もることを考えた。
半径が1(直径が2)の円に内接する(各頂点が円の円周上にある)正六角形と、外接する(円周が各辺に接する)正方形では、「正六角形の周の長さ<円周<正方形の周の長さ」となる。これにより円周率は3よりは大きく4よりは小さいことが証明できる。
ただ、正方形や正六角形の周の長さでは円周との差が大きく「見積もり」が甘い。見積もりの精度をよくするためには、もっと正多角形の頂点の数を増やした方がいいだろう。そうすれば、円と正多角形の間の「隙間」が小さくなって、正多角形の1周の長さは円周により近くなるからだ。
ちなみに、冒頭で紹介した東大の問題は、円に内接する正十二角形を考えればほぼ中学数学の範囲で解決する(他にも色々な解法がある)。計算の詳細は「円周率 3.05」と検索するとたくさん出てくるのでそちらをご覧いただきたいが、概略はこうだ。
まず円に内接する正十二角形のとなりあう頂点と中心を結んで頂角が30°の二等辺三角形を作る。次に、この二等辺三角形の中に補助線を引いて、三角定規になっている有名な直角三角形(3つの角が30°、60°、90°)を作り、三辺の比が1:2:√3であることと三平方の定理を使って、正十二角形の一辺の長さを計算する。最後に、円に内接する正十二角形の周の長さより円周の方が長いことを使って、円周率が3.05よりは大きいことを示す(計算結果には√2や√3が含まれるのでこれらの近似値を使う必要はある)。
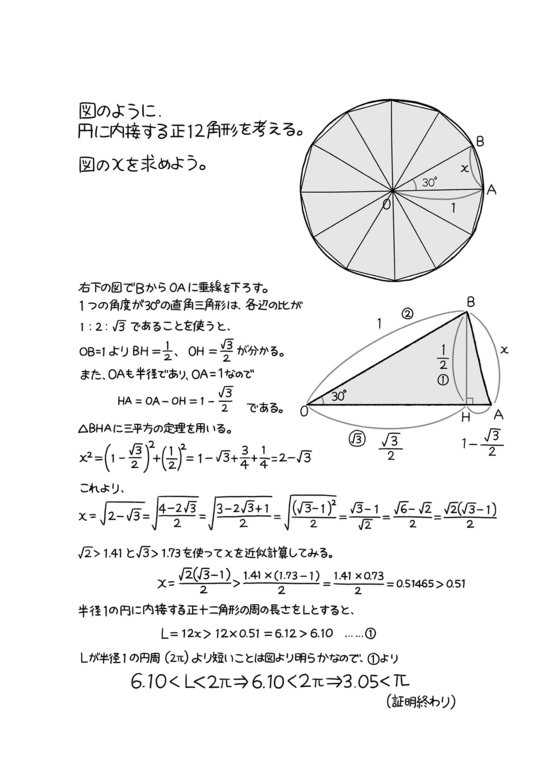 【参考:東大の入試問題の解答例】イラスト:ことり野デス子
【参考:東大の入試問題の解答例】イラスト:ことり野デス子
アルキメデスは、円に内接する正九十六角形と円に外接する正九十六角形を考えることで、円周率が3.1408よりは大きく、3.1429よりは小さいことを突き止めている。小数点以下2桁までは正確な値を求めることに成功したわけである。



