知る人ぞ知る問題解決メソッド、「問題解決の7ステップ」がついに書籍化する――。マッキンゼーで最も読まれた伝説の社内文書「完全無欠の問題解決への7つの簡単なステップ」の考案者であるチャールズ・コン氏みずから解説する話題書『完全無欠の問題解決』（チャールズ・コン、ロバート・マクリーン著、吉良直人訳）が注目を集めている。マッキンゼー名誉会長のドミニク・バートンは「誰もが知るべき、誰でも実践できる正しい問題解決ガイドがようやく完成した」と絶賛、グーグル元CEOのエリック・シュミットも「大小さまざまな問題を解決するための再現可能なアプローチ」と激賞している。本書では、「自宅の屋根にソーラーパネルを設置すべきか」「老後のためにどれだけ貯金すればいいか」といった個人の問題や「販売価格を上げるべきか」「ITの巨人に訴訟を挑んでいいか」といったビジネス上の問題から、「HIV感染者を減らすには」「肥満の流行をどう解決するか」といった極めて複雑なものまで、あらゆる問題に応用可能なアプローチを紹介している。本稿では、本書より内容の一部を特別に公開する。
Photo: Adobe Stock
「完全無欠の問題解決」メソッドで
「どこに住むべきか」に答えを出す
2000年代初頭、チャールズはロサンゼルスに住んでいた。その頃彼は、共同設立した会社を売却したばかりだった。家族は、レクリエーションの機会が多く、学校も充実している小さな街に引っ越したいと考えていた。これまで訪れたことがあるスキー場の街も好きだし、大学のある街に行くのもいつも楽しかった。
しかし、どうやって選べばよいだろうか。非常に多くの変数が関係していて、短期間だけ訪問した印象だけでは、間違った選択をしてしまう可能性がある。そこでチャールズは、日本のキヤノンで働いたときに取り組んだ工場立地問題（こちらの記事参照）を思い出し、同様の方法で意思決定をすることにした。
子どもたちを含め家族全員が、問題解決のためのブレーンストーミングに加わった。各自が大切にしている要因をリストアップすることから始め、この要因が「住みやすい街」を定義した。第一に学校、次に自然環境とレクリエーション、そして最後に街でのクールな体験という順番で、家族は重み付けに合意した。
それからチャールズは、お金の稼ぎやすさという要因を加えた。これらは、家族全員による活発な意見交換の末に合意された。このリストを使って、家族旅行で行きたい街を決めた（図表1）。
図表1 家族ブレーンストーミングのまとめ
チャールズは分析を始めた。まず、問題を家族が大切にしている主な要因に分解し、次に下位の要因を特定し、最後に下位の各要因をとらえる測定可能な指標や変数を特定した。
たとえば、気候変数でいえば、晴天日数や快適性指数（温度と湿度で定義される）といったものだ。少し大変だったが、ほとんどのデータがオンラインで入手できることに気づいた。家族の意見を取り入れながら、彼は各変数に相対的な重み付けをしていった。
チャールズは、約20の変数で構成されるツリーを作成し、約12都市のデータを収集した。彼の作成したツリーは図表2のとおりで、重み付けは太字で示されている。
図表2 「どこに住むべきか問題」を分解する
チャールズが大学のある小さな街や山間部の街のデータを収集したところ、変数の中には繰り返し使われるものや、場所を区別するにはあまり役に立たないものがあることが明らかになった。彼は、分析をより簡単かつ迅速にできるようにツリーを剪定した。その結果、行く必要がない場所も出てきた。
また、空港やハブ空港の周辺にある重要な要因は、「各街から西海岸までの通勤時間」という1つの指標にまとめられることがわかった。チャールズは、若い企業との仕事は、ほとんど西海岸で行っていたのだ。
分析の初期段階ではコミュニティの安全性や犯罪件数といった変数が含まれていたが、これは候補地の差別化要因ではないことが判明したため、これも剪定された。
彼は、各要因のすべてのデータを1から100までの共通の尺度に変換してから、重み付けを適用した。いわゆるデータの正規化にはさまざまなアプローチがあるが、それらはわかりやすく、オンラインで見つけることが可能である。
変数の中には正の傾き（たとえば日照日数は多いほどよい）と負の変数（たとえば通勤時間は長いほど悪い）がある。つまり、マサチューセッツ州アムハーストから西海岸への移動時間の100は負の重みになる。
もし希望するなら「降雨量は欲しいが、多すぎないほうがよい」といったように、変数の重みに複雑な線形をもたせることができる。図表3にチャールズの分析を示した。
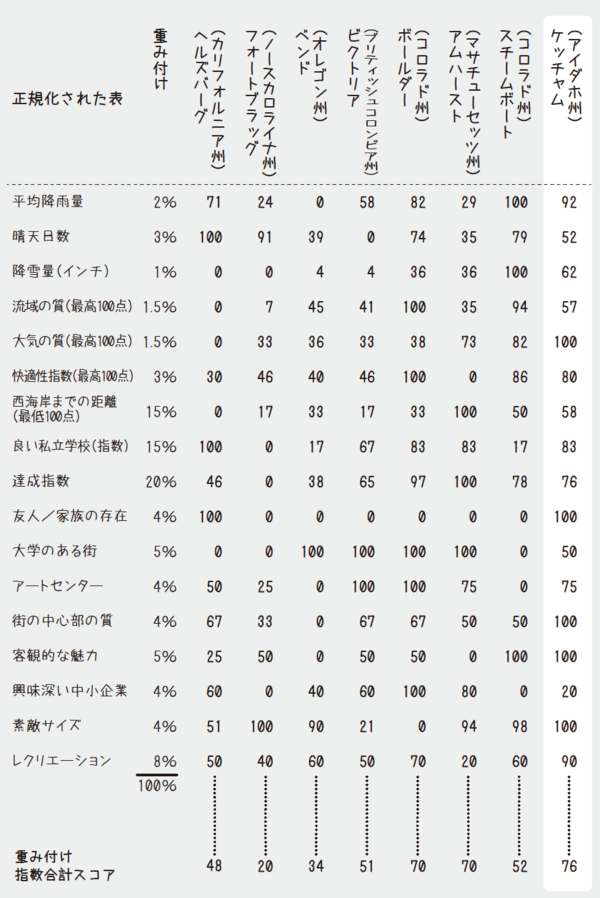図表3 そして最良の街は……？
このケースで家族は、アイダホ州ケッチャムを選ぶという結論に達することができた。住みやすい街を構成する要因は何か、それらをどのように測定し、トレードオフするのかについて合意していたので、家族全員がこの選択に賛成した。
アイダホ州ケッチャムへの引っ越しには大きなトレードオフがあったが、チャールズは受け入れる覚悟ができていた。西海岸への通勤時間が、他の多くの候補地よりもかかるのである。
この例のような体系的な問題解決に対して、最初から考えていたことを証明するためにニセのプロセスを経たのではないかという批判を耳にすることがある。このケースはまったくニセモノではない。ケッチャムは、最初に作成した「検討中の街リスト」には含まれていなかったが、友人を訪ねた後に追加されただけだった。
しかし、この分析にもいくつかリスクを指摘する必要がある。それは、ほんのわずかな差が、数値上の結論に大きな影響を及ぼす可能性があることである。
ボールダー（コロラド州）とアムハースト（マサチューセッツ州）の2都市の総合点はケッチャムに非常に近く、チャールズが「レクリエーション」と「街の中心部の質」を主観的にどのように評価するかというわずかな差しかなかった。
この例では、家族全員がそれぞれの候補の街を訪問し、定量的な変数と比較してどう感じるかを直接確かめることで、リスクを緩和することができる。
このケースでは、問題定義文に関連した論点や要因を簡単なリストにすることから始めて、要因をさらに指標変数［訳注：0か1かのみで表される変数。「ダミー変数」とも］に分解して、最後に具体的な数値測定と重み付けを追加する方法を示した。
あとは、特徴の順位付けに基づいて単純な計算をするだけである。このタイプのツリーと分析のアプローチは、多くの選択問題にも適用できる。チャールズとロブは、この手法を使って、購入するマンション、入社する企業、そしてもちろん工場立地を評価してきた。
（本原稿は、チャールズ・コン、ロバート・マクリーン著『完全無欠の問題解決』を編集・抜粋したものです。この伝説の問題解決メソッドが生まれた経緯はこちらの記事をご覧ください）
