もう1つ例を出しましょう。有名な鶴亀算です。
【問題】
鶴と亀があわせて8匹いて、その足の合計は20本です。鶴と亀はそれぞれ何匹いますか?
この問題の典型的な解法は次の通りです。
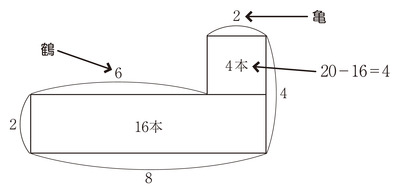
まず、8匹全部が鶴だとすると、足の数は、
8×2=16
より16本となります。
しかし、これは問題文にある20本に対して4本少ないです。一方、鶴1羽と亀1匹を交換すると足の数は2本増えます。4本の差を交換によって補いたいので、
4÷2=2
より、鶴2羽と亀2匹を交換すればよいことがわかります。
よって、
8-2=6
0+2=2
から、鶴は6羽、亀は2匹です。

鶴亀算は次のような面積図を用いた解法も一般的です。
いかがでしたか? 覚えていましたか? でも、ここでは鶴亀算を覚えていたかどうかはどうでもよいことです。問題は、算数で小学生がこの方法を習うとき、多くの場合「なぜこのようにすると解けるのか」を考えていないことです。
もちろん小学校や塾の先生の中には算数の授業の中で「なぜこうすると解けるのか」を熱心に教える先生もいらっしゃると思います。そういう先生は最初に極端な例(全部鶴だと考える)を想定してから実際の事例に沿うように補正していくという考え方の応用性にまで話が及ぶ授業をされていることでしょう。
ただしこの場合、先生は算数を通して「数学」を教えていると言っても過言ではありません。算数を算数として、あるいは中学受験を突破するための技術として教えるのであれば、「こういう問題はこういう風に解くんだぞ」と教え、生徒が典型的な問題を典型的な解法で解けるようになれば、そしてほんの少し応用ができれば、それで十分です。
ちなみに小中高一貫校に通わせてもらっていた私自身は鶴亀算を習いませんでした。なぜならこういった特殊算を使って解く問題はすべて、中学数学で学ぶ方程式によって解くことができるからです。
では、なぜ特殊算を学ぶ必要があるのでしょうか?おそらくそれは、特殊算を用いるような問題でなければ中学入試で生徒の能力を差別化できないからだと思います(私は、中学入試は専門外ですのであくまで推測ですが)。また、中学入試でも一部の上位校では典型的な解法で解くことを想定された問題だけではなく、「考える力」を試す問題が出題され、数学に繋がる素養が測られているようです。