天秤であと何回計れば
仲間はずれが見つかるのか
●1回目に釣り合わなかった場合
Sの4個が上がって、Tの4個が下がったとします(なお、Sの4個が下がって、Tの4個が上がった場合は、同様な議論をSとTを反対にして行えばよいので省略します)。この段階で、Uのオモリはすべて正常です。また、Sに軽いオモリがあるか、Tに重いオモリがあるか、そのどちらかが成り立ちます。
2回目は、天秤の左にSから3個とTから1個のオモリを乗せ、天秤の右にはSから1個とUから正常な3個のオモリを乗せます。
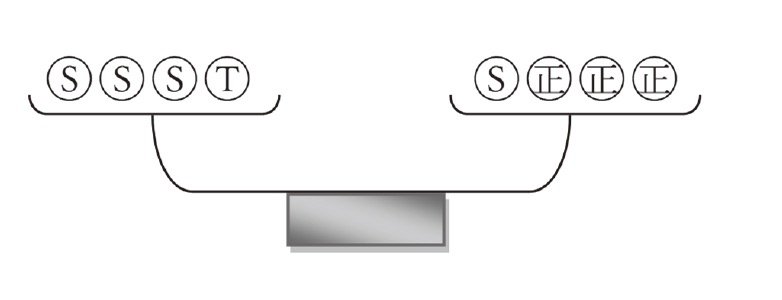 同書より転載 拡大画像表示
同書より転載 拡大画像表示
さらに以下、(ア)、(イ)、(ウ)に分けて考えます。
(ア)左が上がって右が下がる場合
左に乗せたSからの3個のオモリに軽いものがあるので、あと1回で異常なオモリを決定できます。3回目は、その3個のうちの2個を天秤の左右に分けて載せればよいです。
(イ)釣り合った場合
 『数学の苦手が好きに変わるとき』(筑摩書房)
『数学の苦手が好きに変わるとき』(筑摩書房)芳沢光雄 著
2回目に乗せなかったTのオモリ3個のどれかに重いものがあるので、あと1回で異常なオモリを決定できます。3回目は、その3個のうちの2個を天秤の左右に分けて載せればよいです。
(ウ)左が下がって右が上がる場合
この状況では、2回目に左に乗せたTの1個のオモリか、右に乗せたSの1個のオモリが異常になるので、あと1回で異常なオモリを決定できます。3回目は、正常な1個と2回目に左に乗せたTの1個を比べればよいです。
これで解答は終わりです。
参考までに、この問題は次の定理のように一般化することができますが、証明は複雑になります(拙著の『離散数学入門』を参照)。
定理nを自然数とし、外見が同一のオモリが
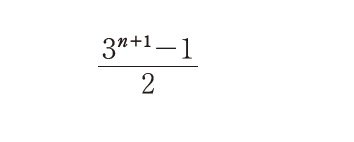 同書より転載 拡大画像表示
同書より転載 拡大画像表示
個ある。そのうちの1つだけ他と重さが違うとし、それは他と比べて軽いか重いかは分かっていない。このとき、天秤をn+1回使ってそのオモリを決定することができる。
以上のようになります。







