試行錯誤する力を身につける
「13個のオモリの問題」
方程式の計算問題のように、「やり方」を暗記してその通りに行うものとは違って、いわゆる「試行錯誤」の問題は、本当は大切です。新たなものを発見したり開発したりするとき、最初は試行錯誤から入るからです。
かつてNHKテレビで、「プロジェクトX」というドキュメンタリー番組があって（2000年3月28日～2005年12月28日）、数多くの試行錯誤を経て成功に辿り着くまでの記録を映し出したものでした。とくに、失敗に次ぐ失敗があっても諦めずに試行錯誤を重ねる精神を見せた点が、戦後日本の成功の秘訣を示したと考えます。
ここで紹介する「13個のオモリの問題」は、まさに試行錯誤の問題で、粘り強くいろいろ試す力を付ける良問でしょう。
【問題】外見が同一のオモリが13個あり、そのうちの1つだけ他と重さが違うとする。そのオモリを「異常」と呼ぶことにして、その他12個のオモリは「正常」と呼ぶことにする。なお異常なオモリは、正常なオモリと比べて軽いか重いかは分かっていない。天秤を3回使って、異常なオモリを決定する方法を述べよ。
【解答例】（最初は4個と4個で比較しなくては解決しない）まず全部のオモリ13個を、4個のオモリの集合Sと、4個のオモリの集合Tと、その他の5個のオモリの集合Uに分けます。そして最初は、SとTで比べます。
●1回目に釣り合った場合
SとTの集合のオモリは正常なオモリとなり、Uの中に異常なオモリがあります。正常と分かったオモリ3個とUの3個のオモリで、2回目を比べます。
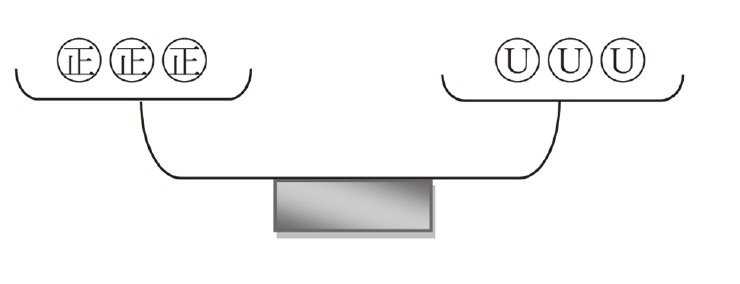同書より転載 拡大画像表示
これで天秤がどちらかに傾けば、たとえばUの3個が上に（下に）動けば、そのUの3個に軽い（重い）ものがあるので、あと1回で異常なオモリを決定できます。3回目は、その3個のうちの2個を天秤の左右に分けて載せればよいです。
2回目も釣り合えば、最後の1回は、正常な1個とUの他の2個のうちの1個を比べればよいです。
