所得の格差は開いていくのか。「ベキ分布」にまつわる問題
公文 ネットワークの話で言うと、スケールフリーネットワークのモデルというのは一部の人が膨大なリンクを持つ一方で、多くの人はごく少数のリンクしか持たないというものでした。こういったモデルでは、グラフはベキ分布に従います。ベキ分布のグラフが成り立つとき、誤差や信頼度についてはどう考えればいいのでしょうか。
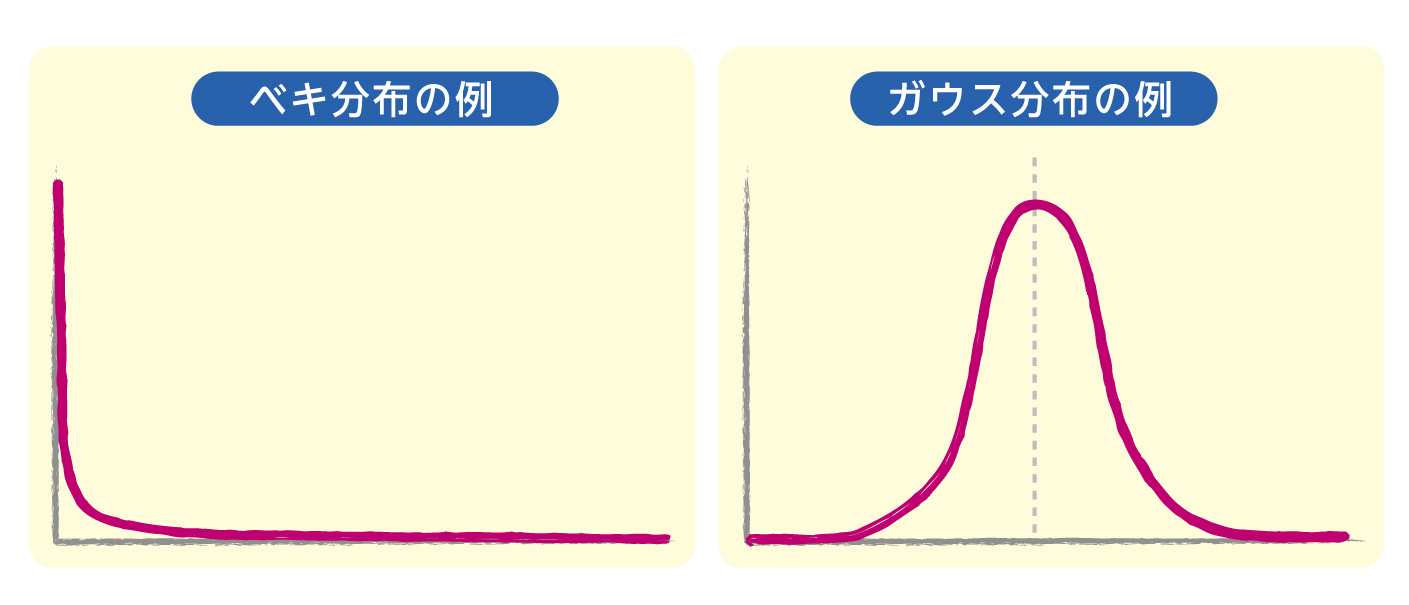
西内 そこはすごく問題ですね。ベル型のガウス分布(正規分布)では起こりえない事象が、実際にはある程度の確率で起こってしまうのがベキ分布です。つまり、とんでもなく大きな値になるという可能性を常に捨てきれない。そうすると、統計学的な推測があまり成り立ちません。
公文 ベキ分布に関連して、ロングテールについて聞いたことがある人は多いと思います。Amazonの売上のほとんどはロングテールから出ているなど、ビジネスに関連しておもしろそうなトピックがいろいろあるからです。しかし、ベキ分布の重要なところは、数値の大きいほうが極端に大きなウエイトを占めているというところで、尻尾の方ではないんですよね。尻尾の方の形について、理論的にわかっていることはそう多くないそうです。
西内 そうですよね。ベキ分布において誤差が発散し、厳密に言えば推定が成り立たない。これは統計学において非常に大きな問題です。これを解決するにはどうすればいいか考えたことがあるんですが、順位に換算すると誤差が収束するということで、一応の解決をみました。
公文 順位に換算する?
西内 例えば、年収のグラフってベキ分布に近いものになりますよね。その確率分布をもとに、父親の年収から子どもの将来の年収を予測するとします。すると、その子がいくらの年収になるかの予測はとんでもなく外れてしまうかもしれませんが、社会全体で上位何%に含まれるかという予測はあまり外れないというような。
公文 なるほど。
西内 所得格差というのは、公衆衛生の世界でも非常に興味を持たれているんですよね。所得の移転問題は経済学でも研究されています。
公文 近年、アメリカでは格差が拡大していると言われていますよね。
西内 一番お金持ちの人と一番貧しい人の間は開いていると思います。でも一度興味があって世代ごとの階層移動のデータを使ってシミュレーションしてみると、だいたいどんな格差も3代たつと消えてしまうんですよ。3代前にお金持ちがいるからといって、あまり安心はできない。格差が受け継がれて、代々格差が開いていくかというと、そうではないという結果になりました。
公文 それはおもしろいですね。古代や中世の社会では、格差は固定し、何代にもわたって富を貯めることができた。だからベキ分布になるというのは考えやすいんですけど、今の情報社会はそうじゃなくなっている。ビル・ゲイツのひ孫はすごく貧乏になっているかもしれません。企業で考えても、マイクロソフトがこの先何十年も持つかはわからない。でもどこからともしれず彗星のように現れた新しい起業家が、天文学的な儲けを得るチャンスはあります。ベキ分布は残っていますが、その中で流動性があるのが新しい。
西内 それは、先生が、近代化は軍事化→産業化→情報化という局面を順番にたどっているとおっしゃっていることに関係が深そうですね。軍事化の時代は土地を中心に、産業化の時代は貨幣を中心に力が生まれていた。土地も貨幣も格差が固定されやすいアイテムですが、情報は流動性が高すぎてとどめておくことが難しい。しかも、新しい情報を得やすいのは若者の特権ですよね。だから、何も持っていなかった若者が急激に富を得て、権力も得るという流れが出てきているのかなと思います。
公文 それが、今の時代のおもしろいところですよね。
◆ダイヤモンド社書籍編集部からのお知らせ◆
『統計学が最強の学問である』 好評発売中!
統計学はどのような議論や理屈も関係なく、一定数のデータさえあれば最適な回答が出せる。そうした効能により旧来から自然科学で活用されてきたが、近年ではITの発達と結びつき、あらゆる学問、ビジネスへの影響力を強めている。こうした点から本書では統計学を「最強の学問」と位置付け、その魅力と可能性を伝えていく。
ご購入はこちら! [Amazon.co.jp] [紀伊國屋書店BookWeb] [楽天ブックス]




