全世界で700万部を売り上げた学び直しシリーズ、「Big Fat Notebook」の日本語版がついに刊行! 大栗博司氏(カリフォルニア工科大学教授)「この一冊で、科学の全貌が見渡せる。中学生のころにこんな本がほしかった」、市岡元気氏(教育系Youtuber)「学校で習う理科がこんなにおもしろいなんてアリエナイ!」、吉森保氏(大阪大学栄誉教授)「カラフルで面白い。ノート風なので読みやすい。大人の学び直しにも最適」と各氏も大絶賛。物理・生物・化学・地学の基本を楽しく一気読みできる本として、大きな話題を読んでいる。
同シリーズの科学版『アメリカの中学生が学んでいる14歳からの科学』の発売を記念して、本文の一部を公開する。
 Photo: Adobe Stock
Photo: Adobe Stock
データの分析と発表
データを整理して発表するための一般的な方法をいくつか紹介しよう。データを縦横に並べて表で示す。数値が隣り合って並んでいるため、素早く読み取って簡単に比較できる。実験の最中にデータを記録するには、もっとも優れた方法。
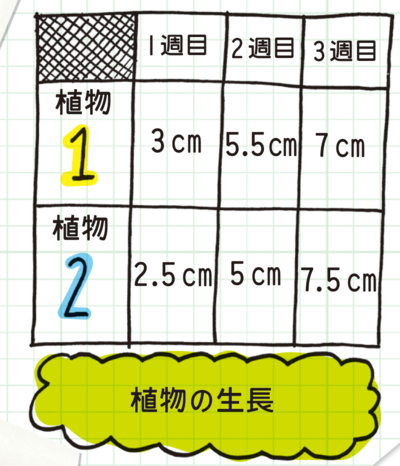
データを表にまとめたら、その情報をさらに見やすくするためにグラフを作る。
1つの変化要素をx軸(水平軸)上に、別の変化要素をy軸(垂直軸)上に表して、2つの変化要素どうしの関係性を示したものを、折れ線グラフという。それぞれの軸の目盛は、測定間隔または測定値の大きさを表す。目盛は等間隔でなければならない。例えば、2, 4, 6, 8...や、5, 10, 15, 20...などとする。2, 5, 7, 15...ではダメ。
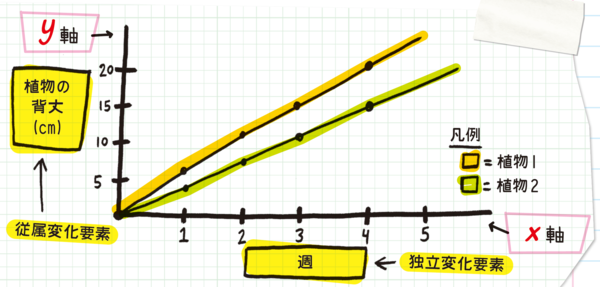
折れ線グラフを使うと、ある変化要素が別の変化要素にどのような影響を与えるか、つまり、独立変化要素によって従属変化要素がどのように変化するかを示すことができる。独立変化要素はx軸上に、従属変化要素はy軸上に表す。植物の生長やレーシングカーの加速など、時間経過とともに連続的に変化する要素を扱う実験には、折れ線グラフがもっとも向いている。
散布図と回帰直線
2つのデータセットどうしの関係性を表したグラフを、散布図という。散布図を作るには、データを順序対として表す(順序対とは単に2つの数のペアのことだが、その2つの数の順番には意味がある)。
例:数学のテストが終わったところで、フィニー先生が生徒たちに、何時間勉強したか聞いた。そしてその回答とテストの点数を記録した。
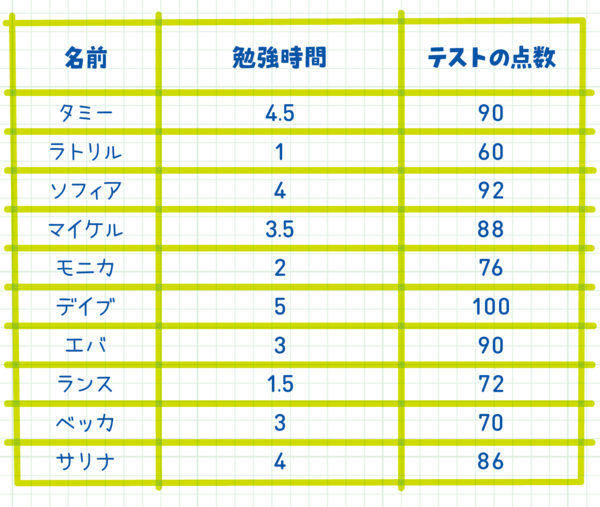
たとえばタミーのデータを記すには、x軸の値が4.5、y軸の値が90である場所に点を打つ。

このデータを散布図で表せば、勉強時間とテストの点数との間に関連性があるかどうかがわかる。見ると、勉強時間が増えるにつれて点数がおおむね上がっていることがわかる。したがって、テストの点数と勉強時間との間には関連性がある。
エバは3時間しか勉強しなかったのに90点取った。ベッカも3時間勉強したのに70点だった。散布図はデータどうしの全体的な関連性を表しているにすぎず、1つ1つの順序対(エバやベッカなど)が全体的な傾向に従っているとは限らない。この場合、エバとベッカは典型的なパターンから外れているので、外れ値とみなせるかもしれない。
この散布図上に、勉強時間とテストの点数との関連性をおおざっぱに示した直線を引くことができる。各点の関連性をできるだけうまく表したその直線のことを、回帰直線という。回帰直線の上にちょうど載っている点は1つもないが、それでもかまわない。回帰直線はあくまでも、散布図のすべての点の関連性をできるだけうまく表したものにすぎない。
棒グラフ・円グラフ
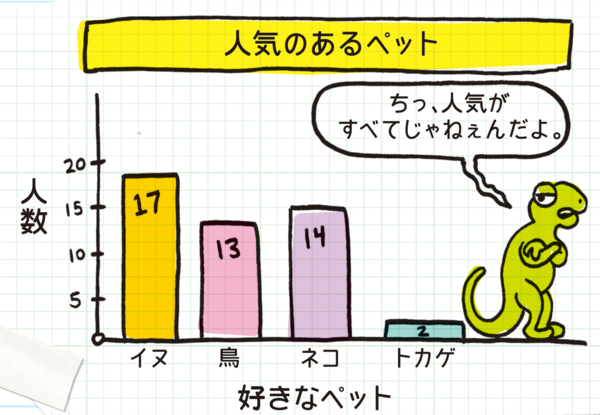
さまざまな高さの長方形を使ってデータを表したものを、棒グラフという。1つ1つの長方形は、ある1つの分類や変化要素、たとえば、飼っているペットの種類や好きなアイスクリームのフレーバーを表している。長方形の高さが高いほど、数値が大きい。
パイを切ったような形をした円グラフというものもある。←うまそうだ!

ほかの人にデータの意味が分かるよう、グラフにはタイトルと、目盛や単位などを付けなければならない。
(本稿は、『アメリカの中学生が学んでいる14歳からの科学』から一部を編集・抜粋したものです)