なぜインドが多くの優秀なエンジニアを輩出しているのか? その秘密は「インド独特の算数教育」に隠されています。インドの算数の授業は、ただ暗記させるだけでなく、なぜそうなるかを考えさせる学習法が基本になっています。どのように計算したらより効率良く正しい答えを導き出せるか、子どもたち自身が考えながら学んでいくことで算数が面白くなり、さらに自発的に勉強が進むようになるわけです。この連載ではそのインド式計算法をわかりやすく学べる本『子供のインド式「かんたん」計算ドリル』の中から具体的な計算メソッドを紹介していきます。
 Photo: Adobe Stock
Photo: Adobe Stock
「1の位が5」で「10の位がちがう数どうし」のかけ算
今回は、「1の位が5」で「10の位がちがう数どうし」のかけ算の計算方法をご紹介します。下の図をご覧ください。
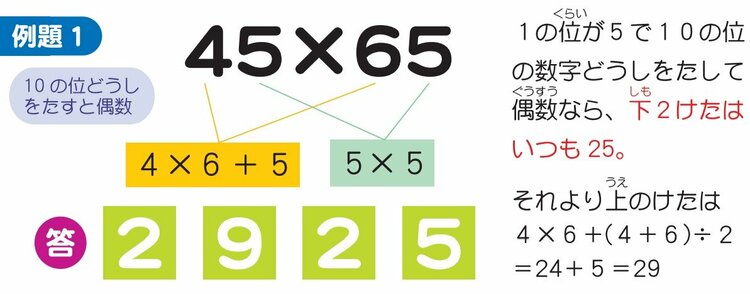
まず、「45×65」のように「10の位の2つの数字をたすと偶数になる場合」は、答えの下2けたが必ず「5×5」の「25」になります。
そして、その上のけたは「『10の位の2つの数をかけた数』+『10の位の2つの数をたした数の半分の数』」になります。
上の図の場合には「4×6+(4+6)÷2=29」です。この「29」と「25」をくっつけて答えは「2925」になります。
次に「10の位の2つの数字をたすと奇数になる場合」を解説します。
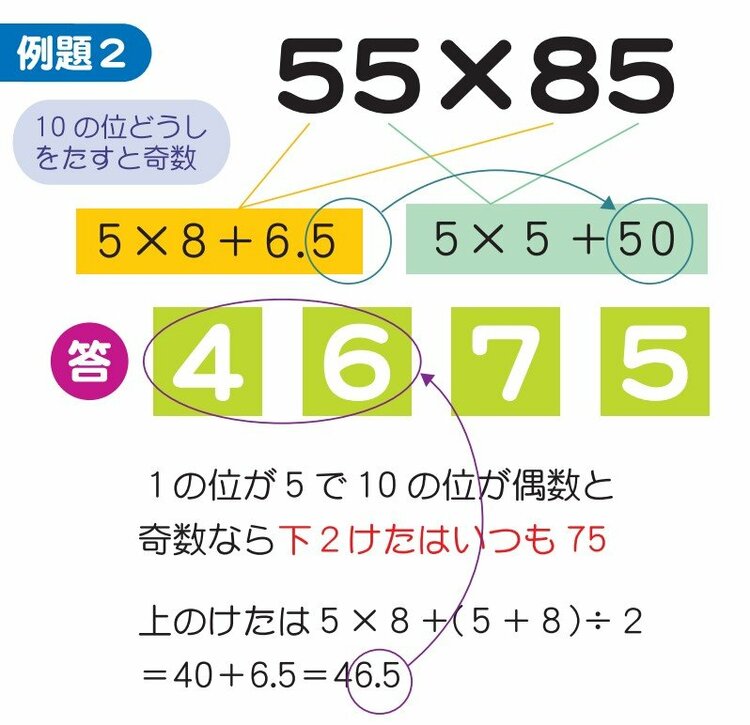
「55×85」のように「10の位の2つの数字をたすと奇数になる場合」は、答えの下2けたが必ず「75」になります。
そして、その上のけたは先ほどの問題と同様で「『10の位の2つの数をかけた数』+『10の位の2つの数をたした数の半分の数(小数点以下切り捨て)』」になります。
なので、この問題の答えは「75」と「5×8+(5+8)÷2=46.5」の「46」をあわせて「4675」になります。
下2けたは「25」ではなく「75」になるのが注意点です。「46.5」のうちの「0.5」が10の位におりてくるので、「25」ではなく「75」になります。
この方法を知っていれば、素早く問題を解くことができるでしょう。
「45×65」を図で考えてみよう

「例題1」の「45×65」を今度は図で考えてみましょう。
そうすると上図のような「5×5の四角形」と「40×60の四角形」と「40×5の四角形」と「60×5の四角形」との4つが集合しているものと気づくことができます。
そうとわかれば、「25+2400+(40+60)×5=2925」とパッと答えを出すことができます。
この問題から「図で考えるメリット」を理解していただけたと思いますが、このような考え方がインド式計算法の極意になります。
もっと問題を解いてみよう
それでは、この方法で他の問題を解いてみてください。

ここに掲載した4問はどれも上の図と同じように考えることで、パッと答えを出すことができます。
問題の答えはこのようになります。
(1)1125 (2)2625 (3)1375 (4)8075
いかがでしたか?
「インド式計算法」は練習すればだれでもマスターできます。ぜひ、挑戦してみてください。



