写真はイメージです Photo:PIXTA
物理学と聞くと苦手意識を感じてしまう人は多いが、意外と身近なものの中に見つけることができる。今回はクレーンゲームの箱型の景品（箱型プライズ）を例にとって、重心と回転の関係性を学んでいこう。※本稿は、小山佳一『クレーンゲームで学ぶ物理学』（インターナショナル新書）の一部を抜粋・編集したものです。
重心の並進運動、重心周りの回転運動
物体の運動はふたつに分けられる
大きさのある物体の運動は、重心の並進運動と重心周りの回転運動に分けることができます。ここでは物体の重心周りの回転運動の一つ、「転倒」について解説をします。クレーンゲームで箱型プライズを転倒させてゲットするイメージで、見ていきましょう。
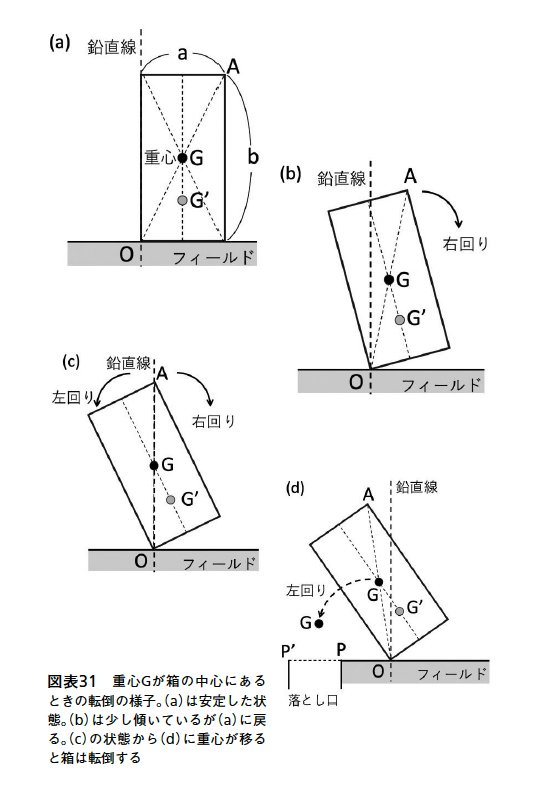
図表31は、箱型プライズの転倒を横から見たときの様子です。図表31（a）のように、幅a、高さbの直方体のプライズがフィールドの上に置いてあります。プライズの重心Gの位置は対角線の交わる位置で、直線OA上にあります。この図では、重力は鉛直下向きにはたらいています。この状況でプライズに外力が作用しなければ、この状態を保ち続けます。
同書より 拡大画像表示
図表31（a）のような状態は、「安定」した状態と言ってもいいでしょう。または、重力によってプライズがフィールドを押す力と、フィールドがプライズを押す力（垂直抗力）が「つり合っている」とも言えます。垂直抗力は、重力の反作用で生じています。
もし何らかの力によって、フィールド上の箱の角の位置Oは変わらず、図表31（b）のように左側に少し傾いたとします。するとプライズは、元の図表31（a）の「安定」な状態に戻ろうと、角Oを回転軸として右回りに回ります。図表31（b）は（a）に比べて「不安定」な状態と見なせますね。
次に、図表31（c）の状態を越えて、図表31（d）のように、左側に大きく傾いた状態になったとします。この状態では、プライズは元の図表31（a）の状態に戻らず、左側に倒れて横倒しになってしまうでしょう。図表31（d）のプライズの状態は「不安定」であり、より「安定」な状態になろうと、箱の角Oを回転軸にして左回りに転倒するのです。
重心が鉛直線を越え
転倒して落とし口に落ちるまで
角Oを回転軸として傾いたプライズが図表31（a）の元の状態に戻るのか、左側に横倒しになるのか？これを決める条件は何でしょうか？
それは、プライズの重心Gが、回転軸となるプライズの角Oから、まっすぐ上に引いた線（鉛直線）を越えるかどうか、なのです。図表31（b）のように、重心Gが鉛直線より右側に残っていたならば、プライズはOを回転軸として右回りに回転して、元の状態（a）に戻ります。一方、重心Gが鉛直線より左側に来た場合、プライズはOを回転軸として左回りに回転し、転倒するのです。
