問題はその権利の値段はいくらになるのかということだ。あなたは「4」が出たのを確認したら、3.5万円を払ってゲームに参加していたことにして、原資産4万円を手に入れる。つまり、利益は0.5万円だ。同様に、「5」が出たときは1.5万円、「6」が出たときは2.5万円の利益となる。
それぞれの確率はすべて6分の1なので、このゲームに後出しジャンケンで参加する権利は0.75万円(=(0.5万円+1.5万円+2.5万円)÷6)となる。
実際にこの後出しジャンケンの権利を7500円で購入したとしよう。この7500円はどんな場合も返還されない(しかし負けて参加料3.5万円をドブに捨てるよりはマシだ)。サイコロの目が1~3だったら、7500円を失うだけで何も起こらない。逆に、4から6が出たら「権利行使」を宣言して3.5万円を支払う。最終的な損益は下のとおり。
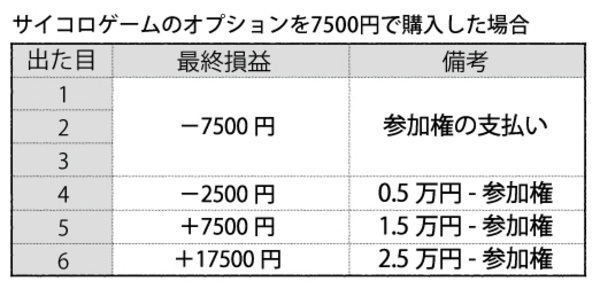
このように、オプションの価値は非常にシンプルに決まる。実際の金融商品でも考え方は同じだ。しかし、株価の場合は、それぞれの価格の発生確率がサイコロの目のように均等になっているわけではない。
たとえば、現在100円でボラティリティ20%の株式があった場合、1年後の株価の確率分布図は下のグラフのグラフの太線のようになる(横軸が株価、縦軸が発生確率)。
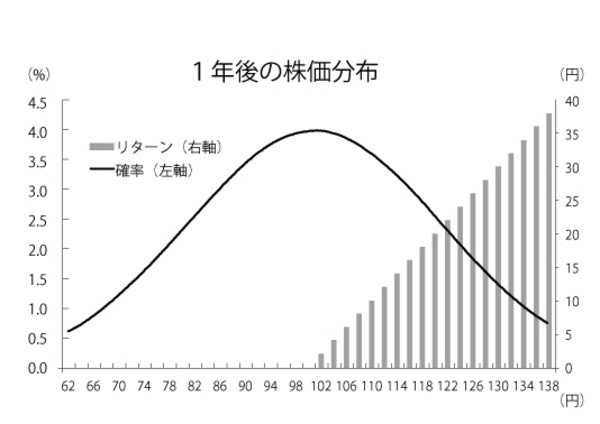
ここでオプションの権利行使価格を、現時点と同様の100円とする。
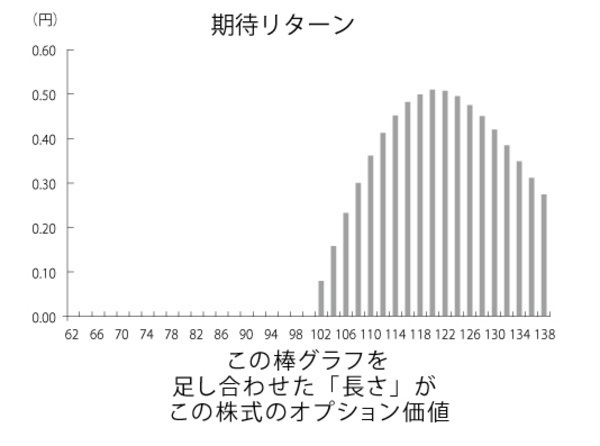
将来の株価から権利行使価格を差し引けば、リターンが出る(網掛けの右肩上がりの直線)。
そのリターンにそれぞれの発生確率を掛け合わせた期待リターン(棒グラフ)をすべて足し合わせれば、オプションの価値は算出できる。つまり、下の棒グラフをすべてつなげた長さがオプションの適正価格なのだ。