多数決の代替案として最適な「ボルダルール」

「民主的な決め方」とは何か

民主主義にもさまざまな考え方があるけれど、その根本にあるのは「被治者と統治者の同一性」だ。これは噛み砕いていうと、自分たちで自分たちのことを決めることだ。「自分だけ」でなく、「自分たち」という点が難しい。

自分だけなら1人で考えれば決定できる。だが自分たちとなると、複数の人がいるから、話はそうシンプルにはいかない。どんなに丁寧に議論を進めても、満場一致の決定に至れるとは限らない。だから集団には、1つの決定を導くための決め方が必要になる。

では決選投票付き多数決と、ボルダルールでは、どちらがより民主的な決め方なのだろう。本来なら満場一致が理想なのだという点は重要だ。すべての人々が選択肢Ａを満場一致で1位に支持するとき、多数決に決選投票が付いていようがなかろうが、ボルダルールだろうが、およそ常識的に考えうるあらゆる決め方はＡを選び取る。実に「自分たち」の決定ができるのだ。

だが、満場一致が成り立たないときには、そもそも全員が満足する決定はできない。決め方を使って多を一に結び付けるのは、本来的に、満場一致からのやむなき妥協であるのだ。

となると、その妥協の程度が弱いもの、満場一致に比較的近い決定ができる決め方を使うのが、「自分たち」の決定をするには相応しい。民主主義は多数派のためのものではなく（ノット・フォー・マジョリティー）、万人のためのもの（フォー・オール）だという考えに親しむ決め方はどれだろう。

満場一致に近い
ボルダルール

先ほどの例でボルダルールは、全員から2位に支持されるＢを選び取る。ではＢを選ぶのは、ほかの選択肢、つまりＡとＣとＤを選ぶよりも、満場一致に比較的近い決定になっているのだろうか。

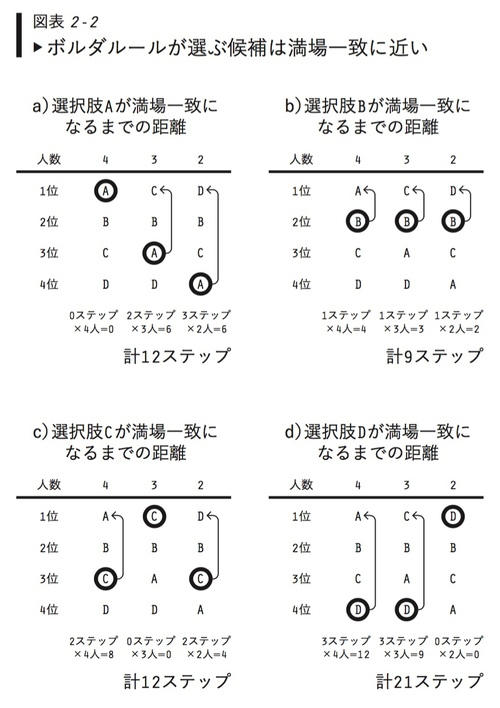
近さとは距離に関する概念だが、ここでは各選択肢について、それが満場一致の1位となるためのステップ数でカウントしてみよう（図表2-2）。

拡大画像表示

まずは選択肢Aを考えてみよう。4人にとってAは最初から1位だ。そこへ3人がＡの順位を2つ上げて、2人がＡの順位を3つ上げると、Ａは満場一致の1位になる。それに要したのは計12ステップ（＝3×2＋2×3）。図表2-2ａは、そのようにして、Ａを満場一致の1位に上げた状況を表している。

同様の作業をＢにしてみよう。9人すべての有権者がＢの順位を1つずつ上げれば、Ｂは満場一致の1位になる。つまりＢは計9ステップの上昇で、満場一致の1位となれる。図表2-2ｂは、そのようにして、人々の順序付けのなかで、Ｂを満場一致の1位に上げた状況を表している。

9ステップで満場一致に到達できるＢと比べると、Ａは3ステップ多く要している。その分だけ満場一致への距離が遠い。

同様に計算してみると、満場一致の1位となるためには、Ｃは12ステップ、Ｄは21ステップの上昇が必要だ。

つまり最少のステップ数、最短の距離で満場一致の位となれる選択肢は、ボルダルールが選ぶＢなのだ。

この例に限らず、ボルダルールが選ぶ選択肢は、必ずそのようになっている。言い換えると、そのような選択肢であらねば、ボルダルールのもとでは絶対に勝利できない。勝つためには広い層からの着実な加点が必要なのだ。この意味でボルダルールは「フォー・オール」の民主主義と相性がよい。

決選投票付き多数決は
「万人のため」の民主主義と相性が悪い

そして決選投票付き多数決が選ぶのは、Ｂと比較すると満場一致に3ステップ遠いＣだ。ボルダルールと比べると、フォー・オールの民主主義との相性が下がる。

付記すると、この相性の悪さは、決選投票とはまた違った「複数回多数決」の方式である繰り返し多数決でも同じである。これは最下位の選択肢を落としながら多数決を繰り返していく決め方で、国際オリンピック委員会が競技種目や開催地の選定でよく使っている。

例えば2020年の夏季オリンピックは東京で開かれるが、その最終選考では東京・イスタンブール・マドリードの3都市が残っていた。そこではまずマドリードが落とされ、次いでイスタンブールが落とされ、東京が勝ち残った。

この決め方は、何度も多数決を繰り返すぶん入念に選定しているように見えるが、「2位以下」が投票用紙に書けない点が、やはり1回だけの多数決と共通している。だから先ほどの例でも、どのみち初回の多数決で1票も得られない「フォー・オール」なＢは、真っ先に落とされてしまう。

ここでの議論はボルダルールが完璧だと主張しているわけではない。満場一致が成り立たない以上、全員を満足させることはできない。ボルダルールはベストではないというより、そもそもベストな選択肢がないから困っている。そこでセカンドベストとして、ボルダルールのもとで勝つ選択肢はきわめて有力ということだ。