多数決には、「票の割れ」という致命的な欠陥があるため、多数派の意見さえ反映されない(詳細は第4回、第5回)。そのため、『「決め方」の経済学』の著者である坂井豊貴氏は、「ボルダルール」という方法を代替案として提案する。なぜなら、「満場一致に最も近い方法」だからだ。詳細を聞いた。
(『「決め方」の経済学』)より、一部を特別に公開します。 初出:2016年7月27日)
スロヴェニアの一部で使われている
「ボルダルール」とは

「1位に3点、2位に2点、3位に1点」のように配点するボルダルールは、18世紀後半にフランス海軍の科学者ジャン=シャルル・ド・ボルダが考案し、はじめて数理的な分析を与えたものだ。
ボルダルールは仕組みとしては単純だから、ボルダ以前にもそれを考案した人はいる。15世紀の神聖ローマ帝国でブリクセン地方の大司教を務めた、ニコラウス・クザーヌスがそうだ。
彼は神聖ローマ皇帝の選出に、「神の意志を見つけるべく」、今でいうボルダルールを用いるよう提言していた(結局は採用されず)。クザーヌスはボルダのような分析は与えていないが、「この方法により、無限に起こりえる過誤を避けられる」と主張していた。
「無限に起こりえる過誤」の真意は不明だが、賢者として知られたクザーヌスのことだから、もしかすると票の割れを気にしていたのかもしれない。
ボルダルールのもとだと有権者は投票用紙に「2位」や「3位」も書けるから、票の割れは起こらない。国政レベルでのボルダルール実用例には、中欧スロヴェニアでの少数民族代表選挙がある。
ボルダルールは多数決とずいぶん異なるように見えるかもしれないが、実はどちらも分類上は「スコアリングルール」という同種に属している。スコアリングルールとは、順位に対して点数を付与する決め方のことだ。多数決は「1位に1点、2位以下はすべてゼロ点」とする極端な傾斜配点のスコアリングルールである。
「ボルダルール」では
「広く支持される人」が選ばれる
決選投票付き多数決とボルダルールは、いずれも、票の割れへの対策が取られた決め方だ。では両者のどこが本質的に異なるのかというと、有権者による「2位以下」の扱い方である。
そこで、候補が乱立するなか「全有権者から2位に支持される候補」を考えてみよう。誰を1位に支持するかは有権者により異なるが、すべての有権者がその候補を2位に支持している。
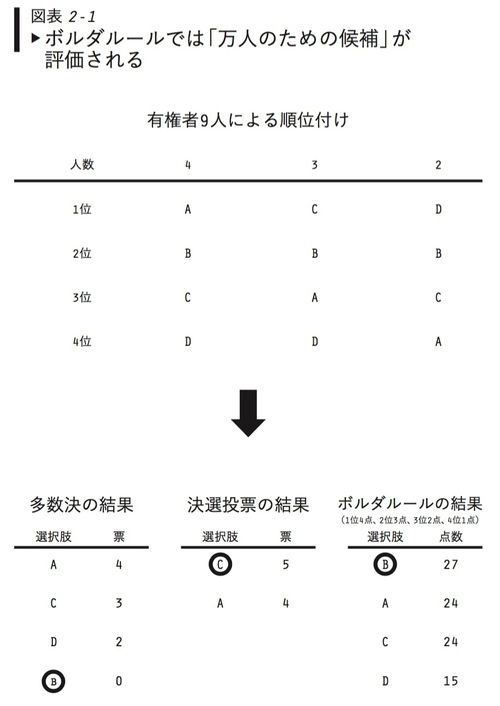
図表2-1の例でいうとBがそうだ。そこでは9人の有権者と4人の候補がいて、すべての有権者がBを2位に支持している。
この例では、ただの多数決だと、結果は上からACDBの順となる(上から4、3、2、0票)。勝つのはAだ。しかし計5人は、CをAより支持している。
だから決選投票付き多数決だと、AとCが決選投票に進んで、そこでCが勝つことになる。決選投票が付いていようがいまいが、Bは最下位である。こうなる理由は明らかで、有権者は1位しか投票用紙に書けないからだ。
一方、ボルダルールだとBが最多の27点を集めて勝つ(AとCは24点、Dは15点)。Bは誰からも1位とされていないが万人からそれなりに高く評価される選択肢であり、そこをボルダルールは汲み取るのだ。
なぜ汲み取れるのかというと、有権者は2位以下の選択肢への順序も投票用紙に表明できるからだ。このことがなぜ望ましいのか、民主主義と決め方の関係から考えてみよう。