横浜元町から汐汲坂を登ると、右手に石造りの重厚な建物が広がるフェリス女学院中学校・高等学校(横浜市中区)
横浜元町から汐汲坂を登ると、右手に石造りの重厚な建物が広がるフェリス女学院中学校・高等学校(横浜市中区)
中学受験の算数は大人にとっても難しい問題が出題される。公開シンポジウム「この数年の難関中学入試/算数&算数オリンピックの注目問題」に関して、前回は「『広尾学園』の算数は何を求めているのか」、という記事を掲載した。今回は横浜を代表する難関校「フェリス女学院」の入試問題を取り上げる。(ダイヤモンド社教育情報)
図形問題が毎回出てくる横浜の名門校
私立女子大学の付属校はおおむね次の3つタイプに分けられる。カトリックの聖心学園や白百合学園に代表されるような、全国各地にある付属・系列校から進学者を集める「総本山型」。難関大学への進学志向を強めて、系列大学への内部進学が半分程度にとどまる「半付属型」。そして、系列大学にはほとんど進まない他大学受験志向の強い「進学型」。
カトリック山手教会、フェリス女子大学と共に、横浜山手にあるフェリス女学院中学校・高等学校は、典型的な「進学型」の付属校だ。
算数の難易度が高いことで有名なフェリス女学院では、女子校にしては珍しく、毎年のように図形問題が出題されている。「角度」「円・扇形・多角形の長さや面積」「体積・表面積」、ときには「展開図」など、問題のタイプも多彩である。
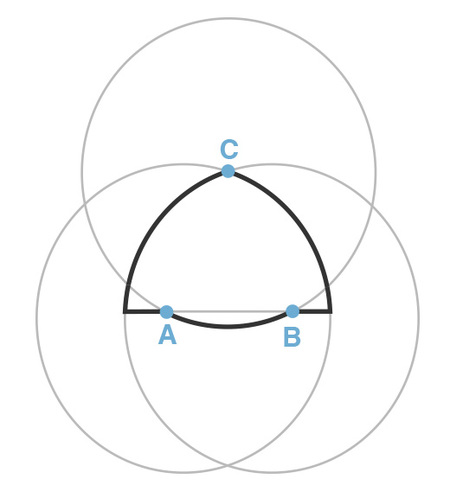
ここでは2019年入試で出題された図形問題を考えてみよう。まずは5分間、じっくりと考えてみて、正答に至らないときには次ページのヒントをご覧いただきたい。
Q 図の3つの円はどれも半径が4cmで、それぞれの中心は点A、B、Cです。点A、Bを中心とする円は、どちらも点Cを通り、直線ABの長さは2cmです。図の太線の長さは__cmです。