天才数学者たちの知性の煌めき、絵画や音楽などの背景にある芸術性、AIやビッグデータを支える有用性…。とても美しくて、あまりにも深遠で、ものすごく役に立つ学問である数学の魅力を、身近な話題を導入に、語りかけるような文章、丁寧な説明で解き明かすロングセラーの数学読み物『とてつもない数学』。鎌田浩毅氏(京都大学教授)「数学“零点”を取った私のトラウマを払拭してくれた」(「プレジデント2020/9/4号」)、「人気の数学塾塾長が数学の奥深さと美しさ、社会への影響力などを数学愛たっぷりにつづる。読みやすく編集され、数学の扉が開くきっかけになるかもしれない」(朝日新聞2020/7/25掲載)、佐藤優氏「永野裕之著『とてつもない数学』は、粉飾決算を見抜く力を付ける上でも有効だ」(「週刊ダイヤモンド2020/7/18号」)、教育系YouTuberヨビノリたくみ氏「色々な角度から『数学の美しさ』を実感できる一冊!!」と絶賛されている。今回は、著者の書き下ろし原稿を特別に掲載する。
2024年現在も未解決の超難問
「現代数学の父」と呼ばれるダフィット・ヒルベルト(1862-1943)はこんな言葉を残している。
「もし私が1000年の眠りから目覚めたら、真っ先にこう尋ねるであろう。『リーマン予想はもう解けたのか?』と。」
また、フェルマーの最終定理を証明したアンドリュー・ワイルズ(1953-)は次のように語った。
「リーマン予想が解けてはじめて、霧の彼方にある広々とした数の大海を調べ、海図をつくる見通しが手に入る。そしてそこから自然の数への理解がはじまるのだ。」
多くの数学者が「もし証明に成功すれば、一つの時代が終わり、新しい時代が始まる」と口を揃える「リーマン予想」とはなにか?
それは、素数の表れ方と深い関係があり、発表から165年が経過した2024年現在も未解決の超難問である。ちなみに、アメリカのクレイ数学研究所は、「リーマン予想」の証明あるいは反証に100万ドル(約1億5千万円)の懸賞金をかけている。
素数は無秩序?
改めて確認しておくと、素数とは「1と自分自身でしか割り切れない2以上の整数」のことをいう。日本語では素数、英語ではprime numberと呼ぶこれらの数は、数の素(もと)であり、物質で言えば、水素や酸素などの元素に相当する非常に重要な数である。
それなのに、「2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37,……」と無限に続く素数がどのような規則で並んでいるのかはわかっていない。
ただ、数学の歴史には、一見無秩序に見える現象から厳密な法則性や秩序を見出した例が数多く存在する。数学者とは、数や図形の世界に美しい秩序があると信じ、それを見つけ出すことに生涯を捧げる人のことだと言ってもいい。
オイラーとガウスの貢献
18世紀に、素数の研究で目覚ましい成果をあげた数学者が2人いる。史上最も多くの論文を書いたレオンハルト・オイラー(1707-1783)と「数学の王様」カール・フリードリヒ・ガウス(1777-1855)だ。
オイラーは、1以上の整数の2乗の逆数(平方数分の1)を無限に足したものは、素数の積で表せることと、その値が円周率(π)の2乗を6で割った数に等しいことを示して、世間を驚かせた(図参照)。
一方ガウスは、なんと15歳のとき、ある数以下に素数がどれくらい含まれるかを見積もる公式を予想した。これを「素数定理」と言う。
リーマン予想とは
ガウスの弟子でもあったベルンハルト・リーマン(1826-1866)が、1859年に発表した「リーマン予想」を数学的に言うと「ゼータ関数の自明でない零点はすべて実部が1/2の直線上にある」となる。
非常に難しい言い回しなので、かいつまんで解説しよう。
オイラーが素数との関係を明らかにした式は、「1以上の整数の2乗の逆数の無限和」だったが、これを「1以上の整数のs乗の逆数の無限和」に拡張したものがゼータ関数だ。
記号ではギリシャ文字のζ(ゼータ)を使ってζ(s)と書く。ここで「s」は複素数であり、複素数は実数(数直線上の数)a,bと虚数単位iを用いて「a+bi」と表せる。aを「実部」、bを「虚部」と言う。
実は、ゼータ関数のsに負の偶数を代入すると必ず0になる(解析接続という特別な手法を使う)。すなわち、ζ(-2)=ζ(-4)=ζ(-6)=…=0である。これらを(全然自明に感じられないが)「自明な零点」という。
ガウスが予想した「素数定理」は1896年にシャルル・ド・ラ・ヴァレ・プーサン(1866-1962)とジャック・アダマール(1865-1963)によってそれぞれ独立に(偶然同じ年に)証明された。
その証明にはゼータ関数の「自明でない零点」の実部が0より大きく1より小さいこと(これは証明済)が使われている。
もし、リーマンの予想どおり、ゼータ関数の「自明でない零点」の実部が必ず1/2であるならば、素数定理の近似精度は飛躍的に高まることがわかっている。
だから、リーマン予想は素数の分布と深い関係がある。
天才達の挑戦を退け続ける「リーマン予想」
リーマン予想の証明にあと一歩のところまで迫ったのは、「ニュートンの再来」とまで言われたゴッドフレイ・ハロルド・ハーディー(1877-1947)と、その相棒ジョン・エデンサー・リトルウッド(1885-1977)だ。
1914年、彼らは実部が1/2の直線上に、ゼータ関数の「自明でない零点」が無限に並ぶことを証明した。ただし「自明でない零点」の中に、実部が1/2ではないものが存在する可能性までは否定できなかった。
ノーベル経済学賞を受賞し、映画「ビューティフル・マインド」のモデルにもなった天才ジョン・ナッシュ(1928-2015)もリーマン予想の証明に挑戦した。しかし、そのあまりの難しさに精神を病み、統合失調症になってしまった。
数多の天才達の挑戦をことごとく跳ね返してきた「リーマン予想」はいつしか「あれには手を出してはいけない」と数学者の間でタブー視されるようになった。「リーマン予想はきっと間違っている」と考える者も出始めた。
しかし、1970年代に入ると、ゼータ関数の零点の分布を表す数式が、原子核のエネルギー間隔を表す式と一致するという衝撃の事実が明らかになる。
自然界の構成要素である原子。その中心にある原子核のエネルギーは、一定にならず飛び飛びの値に変化する。その飛び飛びの値と零点の間隔、つまり原子核と素数が緊密な関係にあるなんて、いったい誰が予想できただろうか。
これをきっかけにして、リーマン予想は再び世界中の数学者達の興味の対象となった。
2020年には、コンピュータを使って、虚部が0より大きく3兆より小さいゼータ関数の零点はすべて、実部が1/2であることが確かめられた。
リーマンが感じ取った素数の中に潜む美しい秩序。それが明らかになったとき、私たちは創造主が奏でる宇宙のハーモニーを聴くのかもしれない。
(本原稿は『とてつもない数学』の内容と関連した書き下ろしです。)
永野裕之(ながの・ひろゆき)
永野数学塾塾長
1974年東京生まれ。父は元東京大学教養学部教授の永野三郎(知能情報学)。東京大学理学部地球惑星物理学科卒。同大学院宇宙科学研究所(現JAXA)中退後、ウィーン国立音大へ留学。副指揮を務めた二期会公演モーツァルト「コジ・ファン・トゥッテ」(演出:宮本亞門、指揮:パスカル・ヴェロ)が文化庁芸術祭大賞を受賞。主な著書に『大人のための数学勉強法』(ダイヤモンド社)、『東大→JAXA→人気数学塾塾長が書いた数に強くなる本』(PHP研究所)など。これまでに1000人以上の生徒を数学指導してきた実績を持ち、永野数学塾は、常に予約キャンセル待ちの人気となっている。NHK(Eテレ)「テストの花道」出演。朝日中高生新聞で『マスマスわかる数楽塾』連載(2016ー2018年)。朝日小学生新聞で『マスマス好きになる算数』連載(2019ー2020年)。『
とてつもない数学』(ダイヤモンド社)がロングセラーとなっている。
数学は、美しくて、深遠で、役に立つ――著者より
1から1000に増えるまでには約2ヵ月かかった。その後、11日で2000にまで増えた。さらに、3日後には、3000を超えてしまった。
これが何の数字かおわかりだろうか? 新型コロナウイルスの日本国内における感染者数の推移である。WHOによると、新型コロナウイルスは1人の感染者からおよそ2人(正確には1.4~2.5人)に感染するそうである。これは、感染者の数が1人→2人→4人→8人→16人……と「倍々ゲーム」で増えていくことを意味する。
「倍々ゲーム」を1から始めた場合、「→」を4回重ねても16にまでしか増えないが、10回重ねると1024まで増える。「→」を20回重ねれば、なんと100万を超えてしまう。このように同じ数を繰り返し掛けることによる変化を「指数関数的変化」と呼ぶ。最初はゆるやかにしか増えないのに、途中から爆発的に増えるというのは、指数関数的増加の最大の特徴だ。冒頭に紹介した感染者数の推移はまさにこの特徴にあてはまる。
もし数学がなかったら、私たちはかつて経験したことのない事態に見舞われたとき、ただ呆然と立ち尽くすか、「予言者」を名乗る人物の言葉を信じるしかないだろう。しかし、数学があれば、たとえ未曾有の感染病であっても、モデルを作り、論理的考察を重ねることで、確度の高い予想を立てることができる。それは未知の問題を解決する緒になる。
現代は、第四次産業革命の真っ只中にある。コンピューターとインターネットの普及によって、AI(人工知能)、IOT(モノのインターネット)、ビッグデータなどが産業に大きな変化をもたらしているのだ。そうした中で、数学の存在感は益々大きくなっている。国家や企業の命運を左右する戦略の決定から、ごくごくプライベートな問題に至るまで、数学の守備範囲は極めて広い。
たとえばイギリスの数学者ピーター・バックスは、2009年に「なぜ僕には恋人ができないのか?」という論文を書いた。その中で彼は、いわゆる「フェルミ推定」を使い、自分が理想とする女性がロンドンには26人いるはずだと算出している(ロンドンの人口を考えると、そのうちの誰かと出会える確率は極めて低いと結論した)。
「フェルミ推定」というのは、既知のデータといくつかの推定量を掛け合わせてだいたいの値をはじき出す手法のことを言う。GoogleやMicrosoftなどが入社試験に「東京にはマンホールがいくつあるか?」のような問題を頻繁に出したことから「フェルミ推定」は注目を集めるようになった。
また、つい最近、こんなニュースもあった。京都大学数理解析研究所の望月新一教授が8年前に書いた「ABC予想」についての論文の査読(内容チェック)が終わり、その正しさが確認されたという。誠に素晴らしいことであるが、このニュースを聞いて「正しいかどうかを判定するのに8年も?」と驚かれた方は多いのではないか。この論文は、発表された当時「理解できる数学者は10人もいないだろう」と言われた。数学はときに、世界最高ランクの頭脳が束になっても叶わないような高い知性を必要とする。
この度上梓させていただく『とてつもない数学』には、数学の、こうしたとてつもない懐の広さと魅力について書いた。数学の学問としての奥深さ、美しさを体現する芸術性、実学としての社会への影響力などを、文系の読者にも読みやすいように、できるだけ噛み砕いて書いたつもりである。また、ことり野デス子さんの可愛く、それでいて数学的に的を射たイラストもふんだんに盛り込まれているので是非お楽しみいただきたい。
歴史に名を残す数学者の姿も書いた。彼らについて知れば、数学は人類が脈々と受け継いできた「叡智の結晶」であることがわかるだけでなく、クールな数式の裏に隠された熱いドラマにも胸を打たれることだろう。
私自身は、高校時代に物理を通して数学の「とてつもなさ」を知った。公式として覚えさせられた数式の数々が、微分・積分によってすべて繋がることを知ったときの興奮と感動は今でもはっきりと覚えている。それは私にとって、数学という世界の扉が開いたような心持ちになる出来事だった。
その後は、数学の持つ合理性と美しさをどこにでも発見することができたし、数学が教えてくれるものの考え方が人生を生きる上での指針になることも知った。
1つの「とてつもなさ」をきっかけにして、こうした経験を積んだことこそ、私が数学の意味と意義とお伝えすることをライフワークにしていこうと決心した最大の理由である。数学の「とてつもなさ」が私の人生を変えたと言っても過言ではない。
本書が、読者にとっての「数学の扉」が開くきっかけになることを願っている。
■新刊書籍のご案内
☆☆信頼のロングセラー3万部突破!!☆☆
鎌田浩毅氏(京都大学教授)推薦!
「数学“零点”を取った私のトラウマを払拭してくれた」
ヨビノリたくみ氏絶賛!
「色々な角度から『数学の美しさ』を実感できる一冊!!」
天才数学者たちの知性の煌めき、絵画や音楽などの背景にある芸術性、AIやビッグデータを支える有用性…。とても美しくて、あまりにも深遠で、ものすごく役に立つ学問である数学の魅力を、身近な話題を導入に、語りかけるような文章、丁寧な説明で解き明かす。文系でも楽しめる究極の数学読物!
数学の概念や理論・方法論は、主に16世紀以降、物理学、化学、生物学、天文学といった基礎科学はもちろん、工学、農学・医学、経済学といった実学にも応用され、さらには哲学や芸術までにも拡がった。そして、第四次産業革命(AI、IOT、インターネット、ナノテクノロジー、自動運転といった技術革新があらゆる場面の産業に引き起こしている技術変革)が進行中の現代では、数学の存在感は益々大きくなっている。
これからは、数学と無関係なものは何もない、と言えるところまで拡大していくのではないだろうか。そういう意味では数学の「とてつもなさ」は、今もなお発展中なのである。
本書では、ピタゴラス、デカルト、フェルマー、ニュートン、ライプニッツ、オイラー、ガウス、カントール……などの天才数学者たちの功績を紹介し、彼らがもたらした方程式、関数、微分積分、集合、確率、統計……といった数学上のブレイクスルーの意味をお伝えした。また、負の数、虚数、無限、N進法といった概念や、円周率やネイピア数という不思議な定数とその影響力の大きさ等についても書いた。
数学の大きな魅力の1つである「美しさ」にも1章を割いたし、魔方陣や万能天秤といったパズル的な話題を通して、数そのものの不思議さが感じられる「計算」も紹介した。我ながらヴァラエティに富んでいると思う。それだけ数学という学問は間口が広いのだ。
本書で紹介した数学の学問としての奥深さ、美しさを体現する芸術性、実学としての社会への影響力などを通して、数学の「とてつもなさ」が――どれかひとつでも――伝わっていますように。そして、あなたにとっての「数学の扉」が開くきっかけになりますように。(本書の「おわりに」より)
 Photo: Adobe Stock
Photo: Adobe Stock
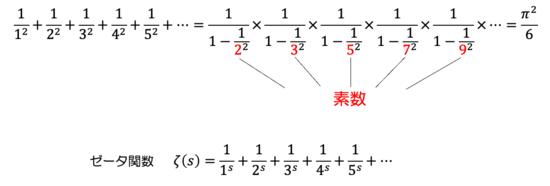 図:オイラーが発見した驚きの数式とゼータ関数
図:オイラーが発見した驚きの数式とゼータ関数







