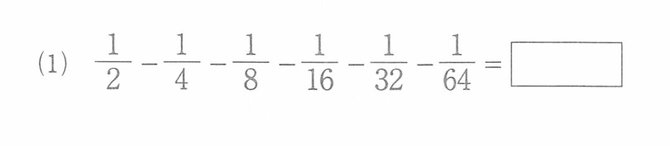中学入試のキモとなるのが算数の問題。学校の求める生徒像がそこには潜んでいる Photo:PIXTA
中学入試のキモとなるのが算数の問題。学校の求める生徒像がそこには潜んでいる Photo:PIXTA
首都圏で最初に一般入試が行われる埼玉の動向は、多くのメディアでも取り上げられ、注目を集めている。これまで志願者動向についてお伝えしてきたが、入試問題にはどのような変化が起きているのだろうか。志願者の多い、栄東と開智の算数の問題を例に、長年入試問題を見続けてきた森上教育研究所「親のスキル研究会」講師である小板橋肇貴氏の解説を交えて見ていこう。(ダイヤモンド社教育情報)
難易度は例年並みだった栄東
首都圏の受験生が腕試しのため受験することもあって、2020年入試でも全国最多の志願者を集めた埼玉の栄東。難易度は例年と変化なかった。
1月10日に行われたA日程の算数の問題から見てみよう。制限時間50分で5問構成。大問1は8つの小問集合。大問2が規則性、大問3が速さの問題、大問4は平面図形、大問5は場合の数となっている。今回の注目問題は大問1(8)と大問3で、それぞれどのように条件を整理していくかによって成否が決まる。
*栄東の問題の解答はこちら。
まず大問1から。□にあてはまる数を答える形式である。
(1)のような、どうすれば楽に計算することできるかを工夫してみるとよい問題は、多くの学校で出題されている。受験生にとってはおなじみのものだ。
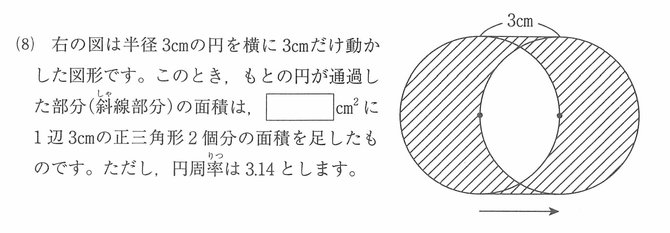
(5)の規則性、(8)の平面図形の求め方を聞く問題で正答できるかが合否を分ける。受験生であれば取りこぼしなく、確実にできるようにしておきたい問題ともいえる。
大問2のような、どういった規則で並んでいるかをきちんと説明しているにもかかわらず、もっと違う視点から見るとどう並んでいるのかを聞かれるような問いかけは、最近の入試問題の流行ともいえる。
これは結局、どういうことを言っているのかを自分の中で消化したうえで考える問題になっている。ただ単純に一問一答形式で対応できる問題ではないだろう。
3つの問いがある。
(1)5段目に初めてライトが点灯したのは何秒後か答えなさい。
(2)11秒後、ライトは全部で何個点灯していますか。
(3)点灯したライトが2020個をはじめて超えるのは何秒後か答えなさい。