「自分の考えや打ち合わせ内容をその場で図解する。このテクニックがあれば、会議、ブレスト、プレゼンが劇的に変わる。考える力と伝える力が見違えるようにアップする」
こう語るのは、アートディレクター日高由美子氏。「ITエンジニア本大賞2021」のビジネス書部門グランプリを獲得した『なんでも図解ーー絵心ゼロでもできる! 爆速アウトプット術』の著者だ。「フレームワーク」や「キレイな絵」を一切排除し、瞬間的なアウトプット力の向上を徹底的に追求するワークショップ、「地獄のお絵描き道場」を10年以上続けている。複雑なことをシンプルに、難しい内容をわかりやすく。絵心ゼロの人であっても、「その場で」「なんでも」図解する力が身につくと評判になり、募集をかけてもすぐキャンセル待ちに。
本連載では「絵心ゼロの人であっても、伝わる図を瞬時に書くためのテクニック」を伝える。
「人数」にフォーカスして、派閥を図解!
菅総理大臣の後任を巡って総裁選の話題が毎日のように報道されています。
前回は「自民党の派閥」と「総裁選の候補者」を1枚の図にまとめました。本日は、派閥の構成比率に焦点を当てて図解します。
参照:前回記事『「自民党の派閥」と「総裁選の候補者」を【1枚の図】にまとめた!』
【参考文献】※クリックで記事に飛びます
●Wikipedia 自由民主党の派閥
●2018年の数値参考:選挙ドットコム(2018/7/17)
「カギを握るのは「派閥に属していない議員」。自民党の各派閥の人数は?」
構成比率を表す型として円グラフや帯グラフがあります。次のイラストを見てください。
円グラフは、全体の中での構成比を円形で示すときに用いられます。特徴としては図形としてインパクトがあり目に入りやすい点があげられます。また、部分相互の比較や、1/2、1/4などの割合は読み取りやすいことが利点といえるでしょう。
気をつけたいのは、項目が多いと細かな分割となり角度の差だけで割合を読み取るのが難しい点です。
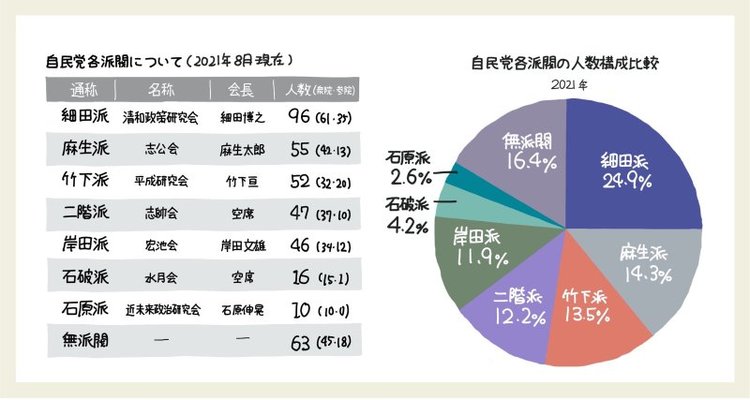
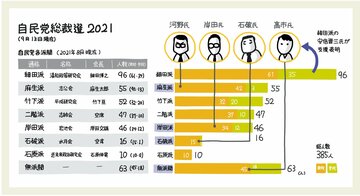
数値から割合を計算してこのような2021年の派閥人数構成比の円グラフを作成しました。円グラフは見た目のインパクトはありますが、棒グラフのように衆議院・参議院の人数もわかるような積み上げの表現はできません。下図を見てください。
円グラフは比較に使える?
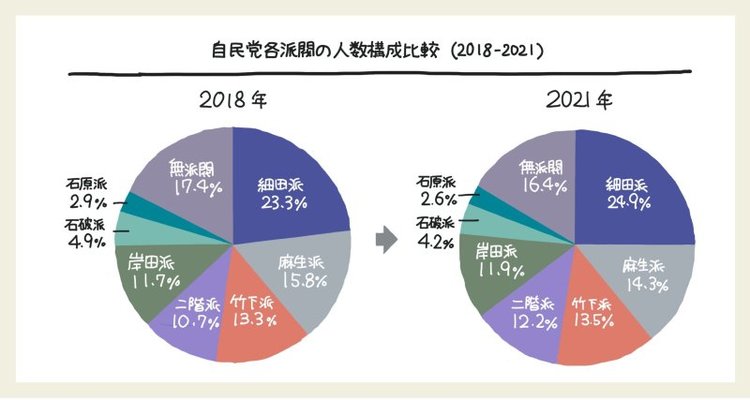
この円グラフ、単体で構成比を伝えることはできますが、時系列での比較に使えるか、検証してみましょう。3年前の2018年の数値を参考にします。
【2018年の各派閥の人数】
細田派(清和政策研究会)96名
麻生派(志公会)65名
竹下派(平成研究会)55名
二階派(志帥会)44名
岸田派(宏池会)48名
石破派(水月会)20名
石原派(近未来政治研究会)12名
無派閥72名
さっそく図にしてみました。下図を見てください。
いかがでしょうか。数値が入っているので内容がわからないわけではありませんが、ぱっと見て変化が伝わる図とはいえません。
円グラフは、構成比を表すとき「特に1項目に注目してその割合をわかりやすく見せる」のに大変適しています。
しかし、このような複数項目の時系列での比較をしたいときには、その差がわかりにくく、見る人を悩ませてしまうことが多いのです。特に今回のように数値の差が顕著でない比較をする場合、「円グラフ」は使い物になりません。
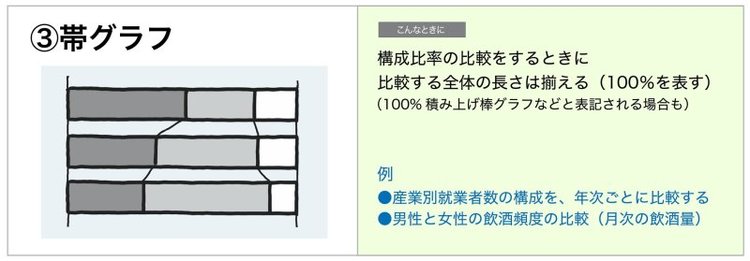
そんなときはこの「帯グラフ」!
複数の構成比を比較したいときは、帯グラフを活用しましょう。次のイラストを見てください。
全体を100%とするところは円グラフと同じですが、同一の内訳を少し細めの線や点線(区分線)で結んで比べやすくできるため、複数のデータを比較するときにも理解しやすく表せます。
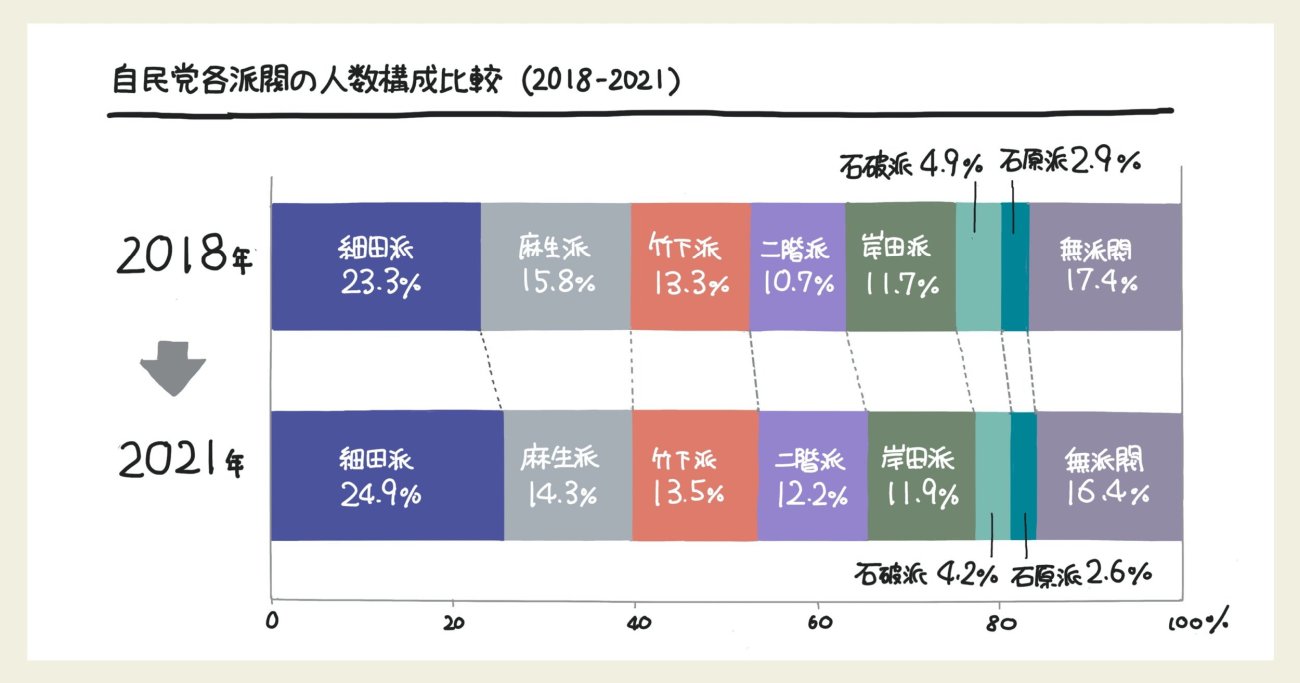
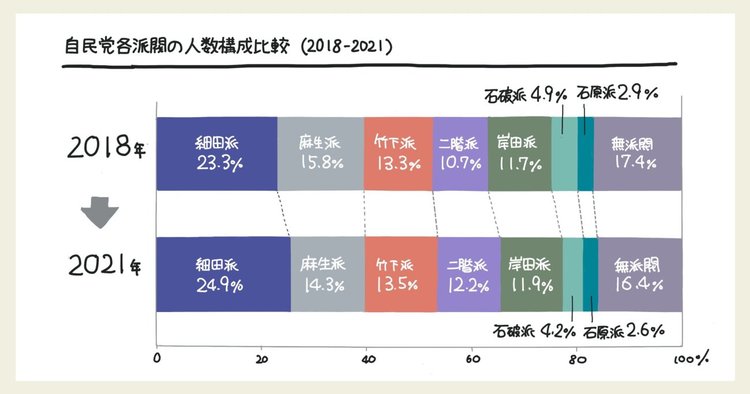
帯グラフは「100%積み上げ縦棒グラフ」「100%積み上げ横棒グラフ」と表記されることもあります。派閥の人数構成の比較を、帯グラフを使ってグラフを作成しました。グラフを見てください。
このように微妙な差でもわかりやすく割合の変化が表現できるため、今回のような「時系列での構成比の変化」を伝えるのは帯グラフがふさわしいといえます。
グラフの用途や役割を理解しておくと、いざPCに向かったときも迷わずグラフを活かした資料作成ができます。
かつて、円盤のようにずらりと並べられた3D円グラフの資料を前にフリーズしているクライアントを目撃したことがありました。複雑な複合型のグラフや3Dのグラフも簡単に作成できる今だからこそ、資料を作るときには基本の型や使う目的をふまえて、「そのグラフは本当に最適か?」を確認しながら作成していきましょう。
日高由美子(ひだか・ゆみこ)
株式会社TAM アートディレクター「えがこう!」代表
東京学芸大学美術科卒業後、日本デザインセンターイラストカンプ部に就職。その後コーセー化粧品宣伝部、ワーナーミュー
ジック・ジャパン編成デザイン部でグラフィックデザインに従事する。1995年より株式会社TAMにてアートディレクターとして勤務。並行して、大阪コミュニケーションアート専門学校非常勤講師としてエディトリアルデザインの講義を行った。絵を描くのが苦手な若手スタッフに「描いて伝える」トレーニングを始め、2015年ごろより社外でもセミナーを開催。「地獄のお絵描き道場」をはじめ、セミナーの総受講者は4000人を超える。グラフィックデザインを通じてのビジュアル構築やグラフィックファシリテーションを得意分野とし、2018年より早稲田大学リカレント教育・WASEDA NEO講師を務める。家電メーカーや外資系ヘルスケア企業・大手銀行シンクタンク・外資系コンサルティング会社などで可視化トレーニングを行う。
重視するのはスピード。「その場で」「なんでも」図解する!
はじめまして。日高由美子と申します。私はアートディレクター(広告やwebサイトなどのビジュアルデザインの責任者)として働いています。
宣伝制作の現場はタイトなプロジェクトが多く、頭の中のイメージやアイデアをブレずに素早く伝えることが重要でした。臨機応変に手を動かし、図解することで課題を明確にし、コミュニケーションをとる。可視化することで説得力も上がり、仕事もスムーズに進みました。
このプロセスを経て、「聞きながら・考えながら」書くことが「スキル」として活かせる手応えを感じました。自分だけのスキルにするのはもったいない。社内のスタッフにもこの技術を伝えたいと思いました。
最初は社内勉強会でしたが、社外からもご要望をいただき始めた「地獄のお絵描き道場」は、開催するたびにキャンセル待ちが出るワークショップになり、のべ4000人を超えるビジネスパーソンに「その場で書いて伝える」スキルを伝えてきました。仕事で実際に活かした受講者の声も届いています。
「説明が上手くなったと、上司から言われました」
「営業資料を検討するオンライン会議で、内容を書きながら共有したら、方向性がすぐ定まりました」
「ふだん議事録を読まない社員が、社内会議に興味を持ちました」
「新商品の開発で、ファン獲得の議論が行き詰まったときに、書きながらブレストをしたら、見過ごしていた問題点が見えました」
この度出版した拙著『なんでも図解ーー絵心ゼロでもできる! 爆速アウトプット術』は、自分の考えや打ち合わせ内容を、その場ですぐ可視化するスキルを解説するものです。「地獄のお絵描き道場」をはじめ、ワークショップでの知見をすべて集約しました。ワークショップの臨場感を出すために、本書は、先生と生徒の対話形式をとりました。絵心ゼロの主人公が、先生の叱咤激励を受け、徐々に「なんでも図解」を体得していきます。
本書を通して、「図解は難しくない」「話しただけではわかり合えないときでも、その場で書けば伝わる」と感じてもらえれば本望です。
本書の主な内容
はじめに 重視するのはスピード。伝わる図を瞬時に書く
INTRODUCTION
・その場で書いて黙らせろ!
・「なんでも図解」5つのメリット
・トレーニングはこう進む!
1日目 「囲み」をマスター! 文字の羅列が一瞬で「図」に変わる
・「なんでも図解」の3大ツール
・囲みでテキストを「図形化」する
・わかりやすさが加速する「囲み」のコツ
2日目 「矢印」をマスター! 関係性を瞬時に伝える飛び道具
・矢印不在の悲劇とは
・矢印はこう書け、こう使え! 流れ、双方向、対立をマスターだ!
・複雑な内容をわかりやすくする「矢印」のコツ
3日目 「人」をマスター! 注目と理解を促す最強のアイコン
・1秒で書ける人のアイコン
・人のアイコンの「2つの使い方」
・喜怒哀楽も1秒で書ける!
4日目 文章を読み、最速で作図する!
・文章を図にする3ステップ
・練習問題1 LINEを図解しよう!
・文章図解トレーニング【初級の6問】
5日目 話を聞きながら図解するコツは「キーワード+余白」
・余白が欠かせない3つの理由
・キーワードをスピーディーに書くコツ
・聞きながら図解するコツ「発言者を明確に」
6日目 会議や打ち合わせでも慌てず図解する
・エリア分けができれば、長い打ち合わせでも図解できる
・3つの型を装備せよ!
・アイコンや絵が多いときこそ時系列を強調
7日目 爆速で書け! アウトプット地獄
・商品やサービスを図解する1「Alexa」
・ビジネスモデルを図解する1「LINE クリエイターズマーケット」
・図解の精度が上がる「5つのテクニック」
・オススメ筆記具
・仕事にすぐ使える 秒で書ける厳選アイコン200
ITエンジニア本大賞2021、グランプリ! 絵心ゼロの主人公と一緒に「なんでも図解」をマスター!
「どうやって図にまとめるか?」も丁寧に解説!