なぜ、2つの「差」をとると
因果関係がわかるのか
なぜ、2つの「差」をとることで、最低賃金の上昇が雇用に与える因果効果を推定することができるのだろうか。例を使って詳しく説明しよう。
あなたは、全国にチェーン展開しているジュエリーショップを経営する企業の広報部長だとする。あなたが勤めているジュエリーショップでは、2014年のクリスマスには広告を出さず、12月の売上は1000万円だった。翌2015年のクリスマス商戦で大々的に新聞広告を出し、12月の売上は1400万円だった。
広告を出すのにかかった費用100万円を差し引いても、2015年12月は前年と比べて300万円分売上が増えたことになる(図表1)。これは広告の効果だと言ってもよいのだろうか。翌年の2016年のクリスマス前にまた広告を出すべきなのだろうか。
 図表1
図表1
実は、この売上の増加は、2つの理由から、広告の効果とは言い切れない。1つめの理由は、時間とともに起こる自然な変化(「トレンド」)の影響を考慮することができないからだ。2015年は2014年と比べて景気がよかったから売上が伸びたのであって、広告を出していなかったとしても売上は1400万円だったかもしれない。
2つめの理由は「平均への回帰」の可能性である。これは、データ収集を繰り返していると、たまたま極端な値をとったあとは、徐々にいつもの水準に近づいていく、という統計的な現象のことだ。このジュエリーショップは、2014年に売上がたまたま減っただけなのかもしれない。だとすれば、平均への回帰が生じ、翌年の2015年の売上は増えても不思議ではない。
では、どうしたら広告の効果を図れるだろうか。そこで登場するのが、今回紹介したカードとクルーガーの研究で用いられた「差の差分析」だ。差の差分析を行うには、介入群(ここでは、「広告」という介入を受けたグループ)と対照群(ここでは、「広告」という介入を受けていないグループ。比較のために用いられる)のそれぞれにおいて、介入前と介入後の2つのタイミングのデータを入手しなければならない。その名が示すとおり、2つの「差」が必要だ。
1つめの差は介入の前後の「差」、2つめの差は介入群と対照群の「差」である。この2つの「差」の差を取って介入の効果を推定するので、「差の差」分析と呼ばれる。
もう少し詳しく見ていこう。図表2で示すように、介入を受けたグループ(介入群)において、介入前の結果をA1、介入後の結果をA2とする。介入を受けなかったグループ(対照群)において、介入前の結果をB1、介入後の結果をB2とする。
 図表2
図表2
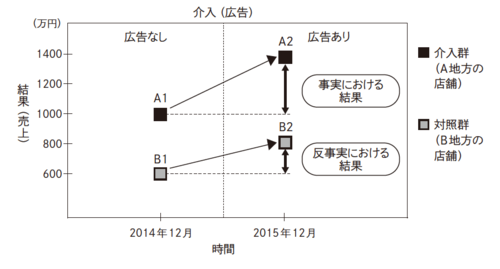
介入群の前後比較(A2 - A1)と対照群の前後比較(B2 - B1)、この2つの差である(A2 - A1)-(B2 - B1)が差の差分析によって推定される介入の効果だ。図表3のA1→Ā2の線が事実(広告を出したシナリオ)を表し、B1→B2の線が反事実(広告を出した店舗が仮に広告を出さなかったらどうなっていたかというシナリオ)を表している。
 図表3
図表3
介入群の前後の差であるA2 - A1から、対照群の前後の差であるB2 - B1を差し引くことで、「トレンド」の影響を取り除き、正しく因果効果を推定することができる。
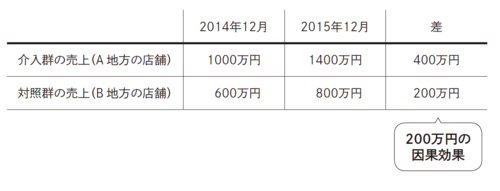
もう一度ジュエリーショップの例に戻ろう。全国にある店舗のうち、A地方の店舗は2015年に広告を出したが、同じ時期にB地方の店舗では広告を出していなかったとする。B地方の店舗では、2014年12月には600万円、2015年12月には800万円の売上となっている(図表4)。
 図表4
図表4
広告を出したA地方の店舗では2014年から2015年にかけて、売上は400万円増加した。一方で、広告を出していないB地方の店舗では800万円−600万円=200万円増加した。この2地方の売上増加幅の差である400万円−200万円=200万円が、差の差分析によって得られる介入の因果効果ということになる。広告にかかるコストが100万円だったしても、広告を出すことで200万円−100万円=100万円の追加的な売上が期待できるということになる。



