開成、麻布、桜蔭、雙葉、筑駒、渋幕……東京・吉祥寺を中心に都内に展開する進学塾VAMOSは、「入塾テストなし・先着順」で生徒を選抜しないが、「普通の子ども」を有名難関校に続々と合格させると話題の塾だ。子どもの特徴を最大限に生かして学力を伸ばす「ロジカルで科学的な学習法」が、圧倒的な支持を集めている。本稿では、VAMOSの代表である富永雄輔氏の最新刊『ひとりっ子の学力の伸ばし方』（ダイヤモンド社）から、特別に一部を抜粋して紹介する。
Photo: Adobe Stock
比が使えないと算数の成績は頭打ち
中学受験の算数問題は非常に洗練されてきており、ただ公式を覚えるだけでなく、根本的な原理原則を理解できていないと解けないものが増えています。
そして、算数の原理原則は「比」にあります。すべての算数の問題は比に行き着くと言ってもいいくらいです。当然、ここを深く学ぶ必要があります。
ちなみに、比についての基本的かつ典型的な例を挙げればこういうことです。
「時速80キロで走る車と60キロで走る車があったなら、同じ時間で進める距離は4：3だが、同じ距離を進むのに必要とする時間は、3：4である」
前者についてはすぐにわかっても、それが後者につながっていかない子どもが多いのです。しかし、それができるかどうかが、あらゆる問題を解く上で大差となって現れます。
正直なところ、算数にはすごく重要な単元とそうでもない単元があり、中学受験までの時間が限られている中で、要領よく学ばせねばなりません。
ところが、兄や姉のときに経験していないひとりっ子の親は、算数についてもまんべんなくカリキュラムどおり学ばせようとします。しかし、比についての理解が低いのならば、どうでもいいことを横に置いて比について学ばせたほうがいいでしょう。
次のページに、天秤の問題を掲載したので挑戦してみてください。「比を使える子どもが中学受験を制する」と言っても過言ではありません。比の概念さえあれば簡単に解けますが、それがないとかなり時間がかかります。
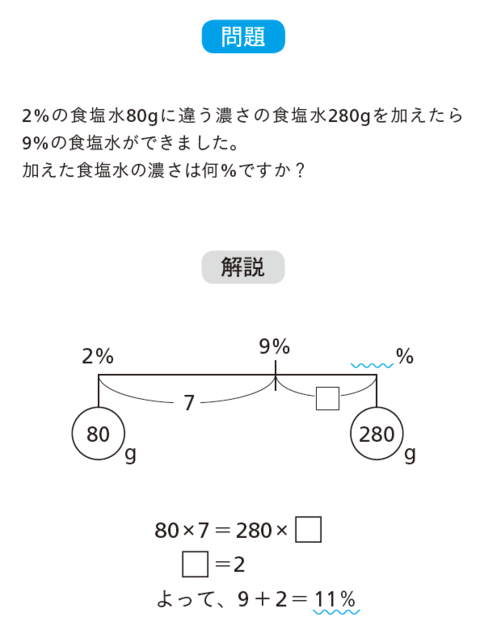「比」が分かれば、簡単に解ける問題
このように、比は算数の問題を解く上で重要な飛び道具でもあり、中学受験だけでなく、高校や大学での数学にも、比の概念は絶対に必要です。
（本稿は、『ひとりっ子の学力の伸ばし方』からの抜粋・編集したものです）
