女子学院の図形問題を解く
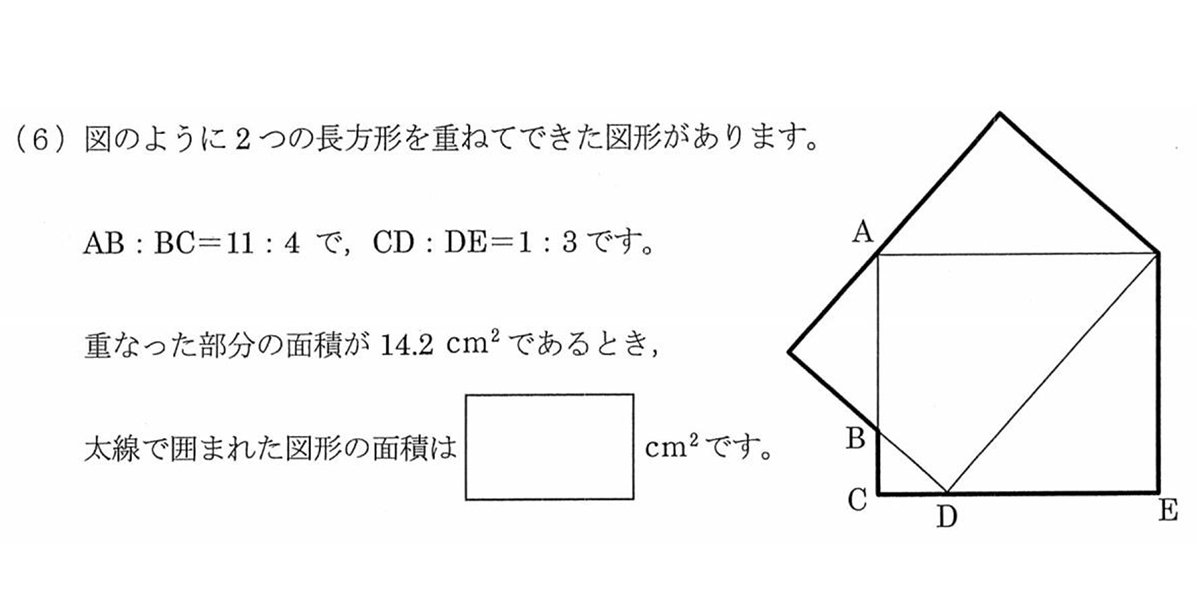
金 女子学院は、いつも図形で、“あれっ”という感じの図形問題が出てくるのが特徴です。今回は、1枚目の大問1(6)を取り上げてみます。これ、意外と苦労すると思います。春日先生、よろしくお願いします。
 春日速水(かすが・はやみ)
春日速水(かすが・はやみ)算数オリンピック委員会事務局長。中学受験指導に精力的に取り組んだ経験をいかし、現在は算数オリンピック大会の運営、問題編集などに携わる。東大農学部卒・同大学院農学生命科学研究科修了。
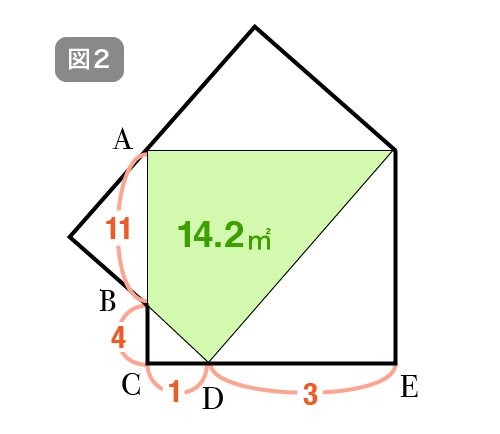
春日 まず問題文にある数値を図の中に書き入れていきましょう。ABが11、BCが4、CDが1、DEが3です。2つの長方形が重なった部分ですから、ABDとEの上でAから右に延びる辺との交点(Fとします)で囲まれた四角形の面積が14.2cm2となります(図2)。
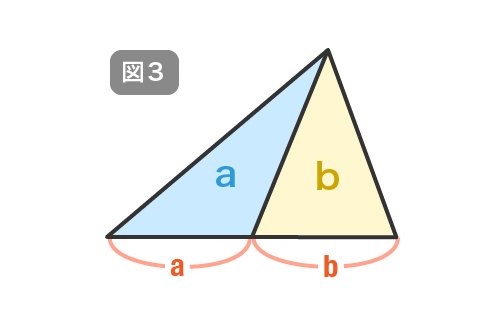
私は、高さが等しい三角形の面積に注目して考えてみました。三角形の頂点から底辺に線を引いて2つの三角形に分けます。図3のように、底辺の比をa:bとすると、それぞれの三角形の面積の比もa:bになります。
では、答えはどのようになるか、考えてみてください。