「1杯目のビール」は2杯目より何倍うまい？数学的に解明した計算結果が超納得だった！

ビール1杯目の幸せを
数式にしてみると……

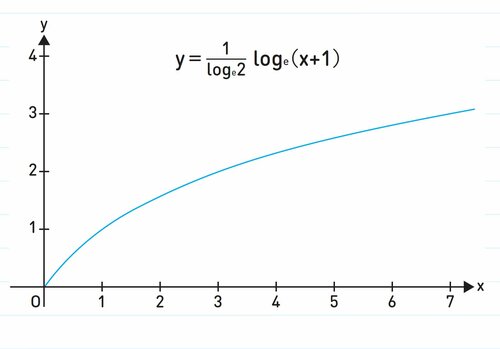
堀口先生　ここで、y＝logexのグラフをかいてみます。（※）ただし、関数の形はわかりやすいようにちょっと変形をしています（y＝1/loge2・loge（x＋1）という式です）。

（※）e：ネイピア数と呼ばれています。2.7くらいの数です。数学的に非常に扱いやすいため、数学ではたくさん登場します。

マリさん　えっとこのグラフはどう見ればよいのですか？

堀口先生　x＝1のとき、y＝1になることは確認できますね。ここから、xが1ずつ増える毎にyの値が増えていくのは確認できるでしょうか？

マリさん　はい。

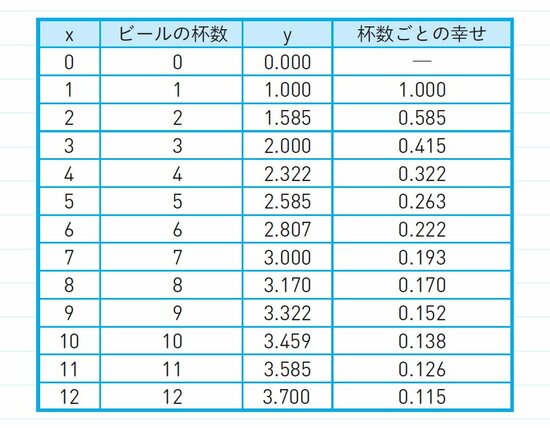
堀口先生　x＝1になるとき、ビールの1杯目を飲んだと考えます。そうなると、yが0から1に増えるので、1杯目の“幸せ”を1と表現できるわけです。

マリさん　なるほど！でも、なぜlogを考えたんですか？

堀口先生　「ウェーバー・フェヒナーの法則」（編集部注：人間の感覚の大きさは受ける刺激の強さの対数に比例する、という法則）ですね。人の感覚は、logでしたよね。

　さて、2杯目についてとらえていきましょうか。x＝2になるとき、y＝1.585くらいとなりますから、ビール2杯の幸せの合計は1.585です。うち、2杯目の幸せは、yの増加分ですので、0.585くらいになりますね。先ほどより減っています。

マリさん　たしかに、2杯目も美味しいですが、ただ、1杯目と比べれば6割くらいになるわけですね。